One of the most common questions that arises from analyses of the global surface temperature data sets is why they are almost always plotted as anomalies and not as absolute temperatures.
There are two very basic answers: First, looking at changes in data gets rid of biases at individual stations that don’t change in time (such as station location), and second, for surface temperatures at least, the correlation scale for anomalies is much larger (100’s km) than for absolute temperatures. The combination of these factors means it’s much easier to interpolate anomalies and estimate the global mean, than it would be if you were averaging absolute temperatures. This was explained many years ago (and again here).
Of course, the absolute temperature does matter in many situations (the freezing point of ice, emitted radiation, convection, health and ecosystem impacts, etc.) and so it’s worth calculating as well – even at the global scale. However, and this is important, because of the biases and the difficulty in interpolating, the estimates of the global mean absolute temperature are not as accurate as the year to year changes.
This means we need to very careful in combining these two analyses – and unfortunately, historically, we haven’t been and that is a continuing problem.
Reanalysis Analysis
Let me illustrate this with some results from the various reanalyses out there. For those of you unfamiliar with these projects, “reanalyses” are effectively the weather forecasts you would have got over the years if we had modern computers and models available. Weather forecasts (the “analyses”) have got much better over the years because computers are faster and models are more skillful. But if you want to track the real changes in weather, you don’t want to have to worry about the models changing. So reanalyses were designed to get around that by redoing all the forecasts over again. There is one major caveat with these products though, and that is that while the model isn’t changing over time, the input data is and there are large variations in the amount and quality of observations – particularly around 1979 when a lot of satellite observations came on line, but also later as the mix and quality of data has changed.
Now, the advantage of these reanalyses is that they incorporate a huge amount of observations, from ground stations, the ocean surface, remotely-sensed data from satellites etc. and so, in theory, you might expect them to be able to give the best estimates of what the climate actually is. Given that, here are the absolute global mean surface temperatures in five reanalysis products (ERAi, NCEP CFSR, NCEP1, JRA55 and MERRA2) since 1980 (data via WRIT at NOAA ESRL). (I’m using Kelvin here, but we’ll switch to ºC and ºF later on).

Surprisingly, there is a pretty substantial spread in absolute temperatures in any one year (about 0.6K on average), though obviously the fluctuations are relatively synchronous. The biggest outlier is NCEP1 which is also the oldest product, but even without that one, the spread is about 0.3K. The means over the most recent climatology period (1981-2010) range from 287.2 to 287.7K. This range can be compared to an estimate from Jones et al (1999) (derived solely from surface observations) of 287.1±0.5 K for the 1961-1990 period. A correction for the different baselines suggests that for 1981-2010, Jones would also get 287.4±0.5K (14.3±0.5ºC, 57.7±0.9ºF)- in reasonable agreement with the reanalyses. NOAA NCEI uses 13.9ºC for the period 1901-2000 which is equivalent to about 287.5K/14.3ºC/57.8ºF for the 1981-2010 period, so similar to Jones and the average of the reanalyses.
Plotting these temperatures as anomalies (by removing the mean over a common baseline period) (red lines) reduces the spread, but it is still significant, and much larger than the spread between the observational products (GISTEMP, HadCRUT4/Cowtan&Way, and Berkeley Earth (blue lines)):
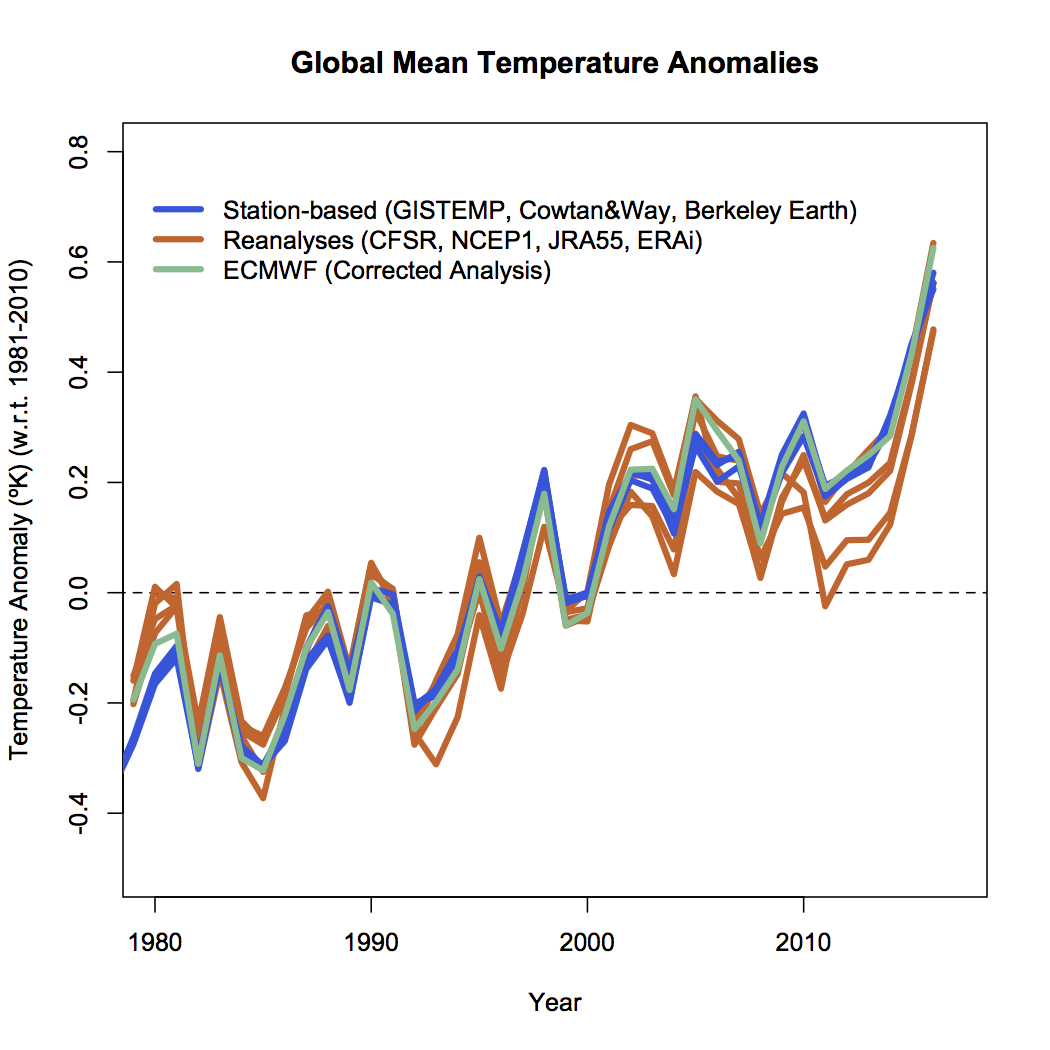
Note that there is a product from ECMWF (green) that uses the ERAi reanalysis with adjustments for non-climatic effects that is in much better agreement with the station-based products. Compared to the original ERAi plot, the adjustments are important (about 0.1ºK over the period shown), and thus we can conclude that uncritically using the unadjusted metric from any of the other reanalyses is not wise.
In contrast, the uncertainty in the station-based anomaly products are around 0.05ºC for recent years, going up to about 0.1ºC for years earlier in the 20th century. Those uncertainties are based on issues of interpolation, homogenization (for non-climatic changes in location/measurements) etc. and have been evaluated multiple ways – including totally independent homogenization schemes, non-overlapping data subsets etc. The coherence across different products is therefore very high.
Error propagation
A quick aside. Many people may remember error propagation rules from chemistry or physics classes, but here they again. The basic point is that when adding two uncertain numbers, the errors add in quadrature i.e.
Most importantly, this means uncertainties can’t get smaller by adding other uncertain numbers to them (obvious right?). A second important rule is that we shouldn’t quote more precision than the uncertainties allow for. So giving 3 decimal places when the uncertainty is 0.5 is unwarranted, as is more than one significant figure in the uncertainty.
Combine harvesting
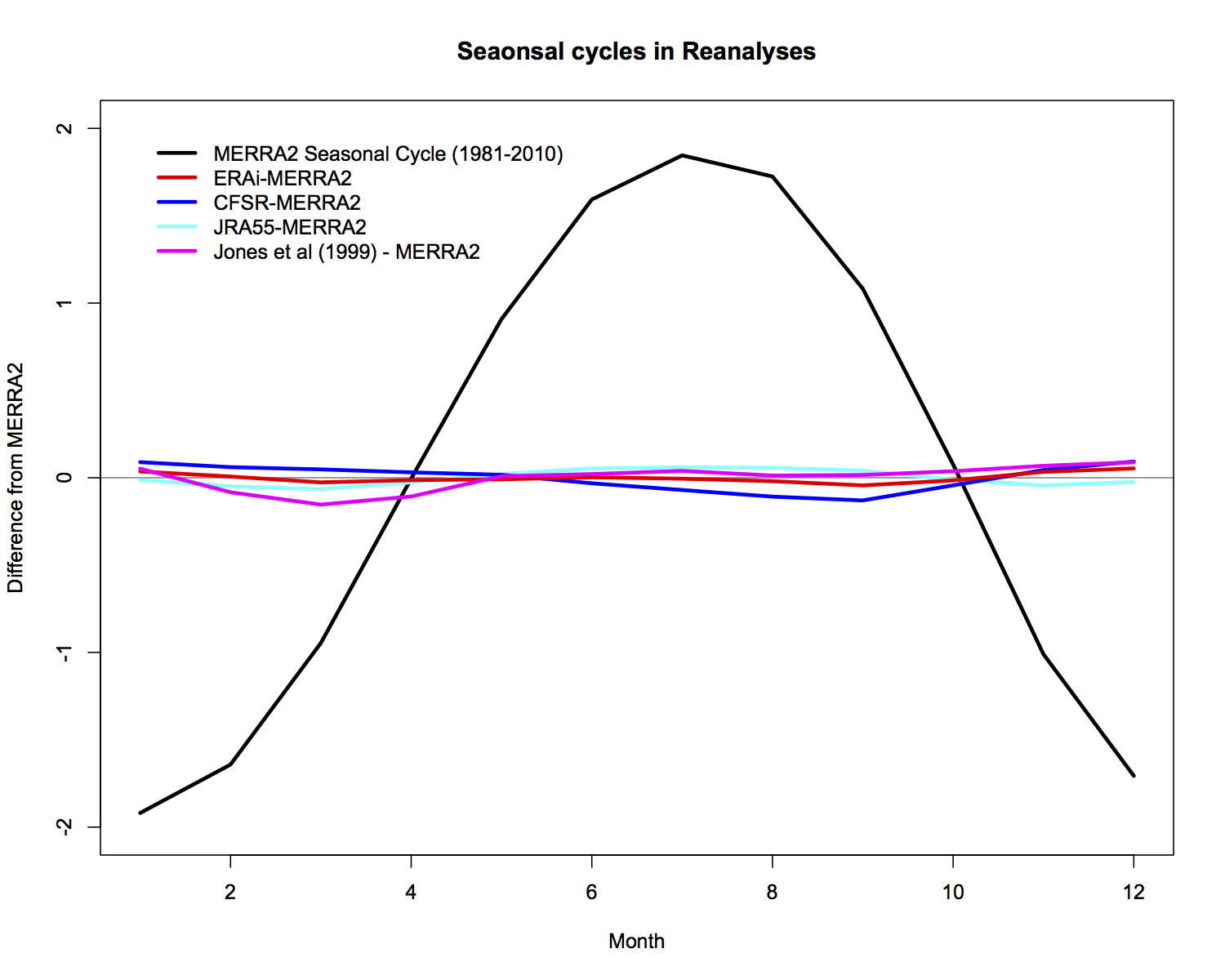
Perhaps surprisingly, the spread in the seasonal cycle in the reanalyses is small once the annual mean has been removed. This is the basis for the combined seasonal anomaly plots that are now published on the GISTEMP website. The uncertainties when comparing one month to another are slightly larger than for the anomalies for a single month, but the shifts over time are still robust.
But think about what happens when we try and estimate the absolute global mean temperature for, say, 2016. The climatology for 1981-2010 is 287.4±0.5K, and the anomaly for 2016 is (from GISTEMP w.r.t. that baseline) 0.56±0.05ºC. So our estimate for the absolute value is (using the first rule shown above) is 287.96±0.502K, and then using the second, that reduces to 288.0±0.5K. The same approach for 2015 gives 287.8±0.5K, and for 2014 it is 287.7±0.5K. All of which appear to be the same within the uncertainty. Thus we lose the ability to judge which year was the warmest if we only look at the absolute numbers.
Now, you might think this is just nit-picking – why not just use a fixed value for the climatology, ignore the uncertainty in that, and give the absolute temperature for a year with the precision of the anomaly? Indeed, that has been done a lot. But remember that for a number that is uncertain, new analyses or better datasets might give a new ‘best estimate’ (hopefully within the uncertainties of the previous number) and this has happened a lot for the global mean temperature.
Metaphor alert
Imagine you want to measure how your child is growing (actually anybody’s child will do as long as you ask permission first). A widespread and accurate methodology is to make marks on a doorpost and measure the increments on a yearly basis. I’m not however aware of anyone taking into account the approximate height above sea level of the floor when making that calculation.
Nothing disappears from the internet
Like the proverbial elephant, the internet never forgets. And so the world is awash with quotes of absolute global mean temperatures for single years which use different baselines giving wildly oscillating fluctuations as a function of time which are purely a function of the uncertainty of that baseline, not the actual trends. A recent WSJ piece regurgitated many of them, joining the litany of contrarian blog posts which (incorrectly) claim these changes to be of great significance.
One example is sufficient to demonstrate the problem. In 1997, the NOAA state of the climate summary stated that the global average temperature was 62.45ºF (16.92ºC). The page now has a caveat added about the issue of the baseline, but a casual comparison to the statement in 2016 stating that the record-breaking year had a mean temperature of 58.69ºF (14.83ºC) could be mightily confusing. In reality, 2016 was warmer than 1997 by about 0.5ºC!
Some journalists have made the case to me that people don’t understand anomalies, and so they are forced to include the absolute temperatures in their stories. I find that to be a less-than-persuasive argument for putting in unjustifiably accurate statements in the text. The consequences for the journalists may be a slightly easier time from their editor(?), but the consequences for broader scientific communication on the topic are negative and confusing. I doubt very much that this was the intention.
Conclusion
When communicating science, we need to hold ourselves to the same standards as when we publish technical papers. Presenting numbers that are unjustifiably precise is not good practice anywhere and over time will come back to haunt you. So, if you are ever tempted to give or ask for absolute values for global temperatures with the precision of the anomaly, just don’t do it!
References
- P.D. Jones, M. New, D.E. Parker, S. Martin, and I.G. Rigor, "Surface air temperature and its changes over the past 150 years", Reviews of Geophysics, vol. 37, pp. 173-199, 1999. http://dx.doi.org/10.1029/1999RG900002
“. I find that to be a less-than-persuasive argument for putting in unjustifiably accurate statements in the text.”
I find it a poor argument for NOAA putting the absolute average in their State of the Climate report. They explain elsewhere why you shouldn’t, and GISS explains it better and more emphatically. But still someone does it. Grrrrr.
I see it as essentially a statistical issue. A station average is a sampled estimate of a population (places on earth) mean. Sampling requires great care if the population is inhomogeneous, to get proportions right. Absolute temperatures are very inhomogeneous (altitude, latitude etc), so great care would be required. But we don’t have much freedom to choose. What we can do is subtract climatology. That doesn’t improve freedom to optimise sampling, but it does greatly improve homogeneity, making it less critical.
I did a sort of ANOVA analysis here to show how subtracting the climatology improved the standard error of the estimate by about a factor of 10. There is a follow-up here.
Missing: UAH and RSS temperatures
[Response: Not relevant to global mean surface temperature. – gavin]
Typo, first para under reananlyses:
“Since weather forecasts (the “analyses”) have got much better over the years because computers are faster and models are more skillful.”
Delete “since”?
JR
[Response: Yes. Thanks. – gavin]
So based on the solar constant, current estimates of albedo and TOA energy imbalance, the absolute temperature of the Earth is about normal, but based on a subjective value of “pre-industrial” Earth has a one degree fever. Plus or minus a half degree or so :)
[Response: No. Warming since the late 19th C is around 1 ± 0.1ºC. – gavin]
Gavin, You make an error common to most physical scientists. If you are talking about the variance of the distribution it remains constant no matter the number of observations . If you are interested in the variance of the mean, in other words how precisely you can believe you know the mean value, that improves as the square root of the number of measurements.
[Response: This is only true if you are drawing from a random sample. Different reanalyses, like different climate models, are not random, and while ensemble averaging reduces errors, it does not converge to ‘truth’ as the number of models is increased. But perhaps I am missing your point? – gavin]
I second what Eli Rabett says. I would also like to say that your claim that “the estimates of the global mean absolute temperature are not as accurate as the year to year changes” is at the very least counterintuitive.
If we look at your error propagation section, we have to note that the error formula for the error of X-Y would be the same; even worse, since this is the formula for absolute, nor relative, errors, the relative error of X-Y can be far worse.
I understand that the anomalies are really used to debias the data, but the way you explain it in this post doesn’t really lead us there. What’s worse, it’s not quite clear from your explanation why exactly ECMWF is a better way to do reanalysis of differences, and, even more, how it manages to combine anomalies specifically so that the aggregate is above (or below) each individual recombination input, as it seemingly contradicts the anomaly recombination approach as a superior one.
Gavin’s response to Eli’s comment sort of relates to my comment about the error propagation equation in the post. That equation is only correct when errors are random – i.e., the covariance between the errors in X and Y is zero. When covariance is not zero, an extra term applies.
When adding two numbers, a positive covariance makes things worse, while a negative covariance makes things better. When taking a difference (i.e. subtracting), the opposite is true.
Thus, when there is a systematic bias (not just random variation), creating a positive covariance between the error values, you can calculate differences much more accurately than the uncertainty in individual values. This is why anomalies work better for changes over time – a station’s systematic bias gets subtracted out (to the extent that it is constant).
[Response: Yes, but in this case we are adding two variables whose uncertainty is independent. There is a stronger case to be made that this matters more when calculating the difference between individual years since the systematic issues in 2015 are basically the same as in 2016, thus the uncertainties there are almost certainly positively covaried, so the formula would overestimate the error in the difference. – gavin]
You’re the best gavin. I think it would be ‘useful’ to put this out as another Ted talk by you to be easily shared via youtube etc (if time permits)
re “Some journalists have made the case to me that people don’t understand anomalies” I get your explanation but what the journos say is still true overall. Isn’t it?
Part of the problem, imo/ime, is the fact that different baseline years for Anomalies are used throughout climate science, for temps but also other aspects, in different papers on the same topic, and thus show up in news reports in the media – for years. That seems to me to also create “consequences for broader scientific communication on the topic [being] negative and confusing.” Yes?
Terms like “Pre-Industrial” as per the Paris +2C limit included are equally vague and/or confusing for the average wood duck aka Journo Pollie Denialist. :-)
Even Warming since the late 19th C is around 1 ± 0.1ºC. is a tad non-specific and vague. Is that 1861-1890 mean? 1890 temp or 1881-1900, or 1880-1920?
So is the term “is around” equally vague, non-definitive and not specific. Hansen Sato would maybe put it as:
“Relative to average temperature for 1880-1920, which we take as an appropriate estimate of “pre-industrial” temperature, 2016 was +1.26°C (~2.3°F) warmer than in the base period.”
http://csas.ei.columbia.edu/2017/01/18/global-temperature-in-2016/
The IPCC says it in other ways as well. It’s variations like this between “scientists” that denier activists and marketing shills can regularly drive a truck of disinformation through which aggravates the confusion even more, imho.
As Hansen also notes in that paper ref above … “The United Nations Framework Convention[v] and Paris Agreement[vi] define goals relative to “preindustrial”, but do not define that period.
Another example – “In this graph the base period is switched from our traditional 1951-1980 to 1880-1920 for the reasons given in “A Better Graph”, but of course we continue to also produce our graphs with the 1951-1980 base period, as shown below.” http://www.columbia.edu/~mhs119/Temperature/
I have seen others using 18th century period as the “real” Pre-Industrial baseline eg 1750. In saying this, I do understand that different periods and comparisons are being made for scientific reasons, as per the 1 mth, 3 mth, 12 mth and 5 yrs running means on the Hansen page – and that also requires different baselines depending on what is being evaluated.
I get that, as do others with an eye for detail .. the avg wood duck does not and never will.
To put it another way Gavin — “Houston, we still have a problem.”
Only the climate scientists, orgs bodies like the NASA IPCC AGU and Universities can fix this collectively themselves to minimise subsequent confusion in listeners and minimise distortions by denier quarters. “How” is something for scientists to advocate for, not me. cheers
Gavin, what you wrote was “Most importantly, this means uncertainties can’t get smaller by adding other uncertain numbers to them (obvious right?).” and what Eli pointed out is that they certainly can if what you are interested in is the uncertainty in the mean. The issue if there is a random component (noise) in the data points. Whether it converges to a true value depends on whether there are systematic variations affecting the whole data set, but given a random component more measurements will converge to a more precise value.
[Response: Yes of course. I wasn’t thinking of this in my statement, so you are correct – it isn’t generally true. But in this instance, I’m not averaging the same variable multiple times, just adding two different random variables – no division by N, and no decrease in variance as sqrt(N). Thanks though. – gavin]
While do not wish to derail the good scientific mathematical discussion here Gavin, I do have another related ‘wish request” for the benefit of the avg person and journos understanding. I do get you and all the rest have better things to do with your time though. nevertheless something like the following may be ‘useful’ overall and long term.
RC or others equally qualified to summarise and then continually update this data to a ‘consistently comparable standard’ including baseline info.
– What’s the mean avg growth in global CO2 and CO2e last year and over the prior ~5 years
– What’s the current global surface temperature anomaly in the last year and in prior ~5 years
– project that mean avg growth in CO2/CO2e ppm increasing at the same rate for another decade, and then to 2050 and to 2075 (or some other set of years)
– then using the best available latest GCM/s (pick and stick) for each year or quarter update and calculate the “likely” global surface temperature anomaly into the out years
– all things being equal and not assuming any “fictional” scenarios in any RCPs or Paris accord of some massive shift in projected FF/Cement use until such times as they are a reality and actually operating and actually seen slowing CO2 ppm growth.
– and if at some time in the future there is a major adjustment to GCMs modelling like plugging in a new science based assumption that x warming will actually/or has triggered negative feedbacks like ASI area/piomass loss, or methane hydrates emissions inott eh atmosphere versus the present GCMs that such changes in the GCMs be noted in these Summary Key data Updates.
– and that every summary ever done is stored and accessible for comparison with later Updates in a way that the average lay person can “see” the trend and direction of Temps and key GHG ppm inn the atmosphere
– one could setup an initial data set that goes back to the year 2000 on the same page so people can see and grasp the changes in “numbers” …. and that’s it. Is CO2/CO2e increasing or decreasing .. is Avg Mean Temp Anomalies increasing or decreasing – side by side, year by year – and what does that tells us about current BAU in 10 years from now, in 2050 and in 2075… everything else being equal?
– I think these are numbers that most people could grasp much more easily the plethora of comparison graphs and numbers across different science websites, blogs and IPCC reports.
– and let the science maths arguments about this “summary” go one behind closed doors with a separate explanation sheet in detail for the more mathematical/science folks to know about.
– K.I.S.S. Principle maybe helpful.
sorry of this is a waste of your time and space here. thx T.
“the correlation scale for anomalies is much larger (100’s km) than for absolute temperatures”
Can someone explain what this means? I don’t have enough of whatever background is involved to know what is being correlated, and what type of (temp?) anomaly is being spoken of.
[Response: The temperature in Montreal is generally much cooler than in New York, but it turns out that if Montreal has a cooler-than-normal month (a cold anomaly), then so did New York. Similarly, if the month was warmer than normal in NYC, it was likely to be warmer than normal in Montreal. The distance over which these connections are useful is about 1000km, as you can see from looking at a single month’s temperature anomaly pattern. This means that you can safely interpolate the anomalies between stations. This doesn’t work well for features that have a lot more small scale structure (like rainfall, or absolute temperatures, or cloudiness) though. – gavin]
I believe it is most ineffective that the scientists and their institutions more or less randomly choose their reference periods.
I asked one of the scientists producing these estimates why the Paris Agreement reference to “pre-industrial” is not used. His response was that “it is not the scientist’s role to take position on political matters”.
“Pre-industrial” is indeed a political choice, but also a choice that definitely already has been made. It has been aproved by all those 198 government representatives who signed the agreement. Some 135 countries have made it part of their national laws by ratifying the Paris Agreement, and therefore it is part of the base on which they design their climate policy and plans. Moreover, it is in general use in the media world wide.
The responsible officials can handle the multiple baselines, one can hope. The general public and the politicians maybe not. Votes are counted, from time to time. A single baseline and a single number would probably be more effective.
The frequently cited IMO/WMO recommended climate computation baseline (i.e. now 1981 – 2010) is basically reset to zero at 10 year intervals. It was designed in 1935 for quite different purposes. Global warming was not a major concern, then.
> unjustifiably accurate
That’s going to confuse the fifth-grade-level reader.
Are there any clearer words for that sense?
Perhaps “unjustifiably exact” or “unjustifiably precise”?
I have another wish — I wish that the Climate Scientists would create a more realistic Charctic and PIOMASS analysis that actually compared the Present with the 1880-1920 Median Baseline for a real ASIE Deviation/Anomaly (as they do for Global Temperature Anomalies)
“One of the most common questions that arises from analyses of the global surface temperature data sets is why they are almost always plotted as anomalies and not as absolute temperatures”
Well, why do they ask? Can the problems be better addressed?
I suspect that the complaints are because the anomalies have little meaning when looking at data for any specific year or other time period. So what if the anomaly is the degree change from 1981-2010? When presenting data aimed at the public it is much better to give the change since the beginning of the industrial era, e.g. 1880-1900. I agree with comments 8 and 12.
Also, I suspect that an important reason why anomalies are used is because it down-plays the difference between the various temperature series. That is, if one series consistently shows more temperature growth than a second series, the difference between the two is parceled between the pre- and post-mean parts of the series. Using 1880-1900 as a base point, the temperature series would depart more in 2017 then using 1981-2010 as the base.
Using anomalies particularly bothers me because is forces one to think of temperature change as linear, whereas it appears to be exponential. That is, once cannot use logs with anomalies, or calculate percent changes.
Suppose one were to measure the IR emission of Earth from say Neptune, to derive the Earth’s effective Black Body Temperature – Teff.
1) Would Teff vary during one (earth) year ?
2) Would Teff have changed at all since 1850 ?
[Response: You don’t have to go to Neptune, you can just degrade the data from DSCOVR (there is a paper on this either out or in press). You’ll see a diurnal cycle (as a function of the continental configuration) and an annual cycle as a function of the imbalance in hemispheric seasonality. As for long term trends, that depends on the energy imbalance. At equilibrium at 2xCO2, Teff could be smaller or larger depending on the SW cloud feedbacks. Assuming that they are small for the time being, you would initially get a *decrease* in Teff as CO2 levels rose (blocking some IR), and then a gradual increase as the surface equilibriated. Given that we are still in the transient phase, I think you’d see a small decrease that would persist. This can be calculated from GCM output from historical runs though, so if I get time I’ll make a plot. – gavin]
gavin, inline to #11:
This is ‘autocorrelation’, amirite?
Me, previously:
More specifically, is it ‘spatial and temporal autocorrelation’?
Although Eli has lost the paper and his memory, there were one or more publications which showed that the distance temperatures correlated varied with the season but were always quite a distance. Given modern computing power it might be interesting to include that in the analyses.
Why do you say absolute temperature when you mean temperature? Temperature and temperature anomaly make sense.
I think this is not a blog for physicists. The physical quantity is the temperature. You can measure it in K, °C, F or something else. Derived quantities are the relative temperature or the the temperature anomaly. When you make a physical model you have to compare the temperature with the model. In principle, you can also compare anomaly with anomaly. But this is not so accurate.
[Response: Actually you are wrong. Modeling and predictions of anomalies are more accurate! – gavin]
Last week I looked for the monthly average temperatures of the Atlantic Ocean NH. Where can I find it?
P. Berberich:
Physicists often say that 8^)! It’s actually a blog for earth scientists. Physics is a foundation of climate science, but climate science does not merely reduce to physics.
re 14 Thomas; aha, I see much of the necessary data record work has already been done. https://nsidc.org/data/g10010 and a 2016 report https://www.carbonbrief.org/guest-post-piecing-together-arctic-sea-ice-history-1850
hat tip to Florence Fetterer et al – https://www.realclimate.org/index.php/archives/2017/08/data-rescue-projects/#comment-681981
Excellent work and great to know. Maybe it would still be useful to see the numbers of mean/anomaly changes over time for comparison with the present and then communicate the implications of that? It appears that summer sie began falling in a constant noticeable ‘manner’ in the 1920s. Interesting.
@22
The raw data are available as equal area grid values from https://data.giss.nasa.gov/gistemp/ (see ERSSTv5near the bottom of the page).
It will take some significant work to assemble the subset you want. Probably someone out there already has and may come forward. You might try posting this request at https://moyhu.blogspot.ca/ a blog which often discusses these sorts of issues.
@P. Berberich
usually it is far more accurate to measure difference or anomalies then absolute values. Not only for temperatures but also for weights, lengths, velocities and so on.
@26:
“Usually it is far more accurate to measure difference or anomalies then absolute values. Not only for temperatures but also for weights, lengths, velocities and so on.”
Usually you measure the mass, the length, the temperature, the velocity and afterwards you calculate the difference. Perhaps, you want to say that the calibration is a process where differences are measured and made to Zero.
“Although Eli has lost the paper and his memory, there were one or more publications which showed that the distance temperatures correlated varied with the season but were always quite a distance. Given modern computing power it might be interesting to include that in the analyses.”
There are several papers. It varies with season, it varies with latitude and of course varies with longitude because, well, oceans.
hmm one paper on GHCN daily comes to mind, but I’m losing my memory as well.
there was also a great paper on the Arctic that i can probably find.
and of course the correlation distance can be greater in one direction ( east or west ) than the other direction. it blows.
P. Berberich in #27 says: “Usually you measure the mass, the length, the temperature, the velocity and afterwards you calculate the difference. Perhaps, you want to say that the calibration is a process where differences are measured and made to Zero.”
I suspect Uli meant exactly what he said. There are many situations in which it is best to measure all kinds of quantities as differences, not as absolute values; and where directly measured differences are more accurate than absolute values that would need to be subtracted to calculate a difference. I suspect we might be seeing some illustrations of this.
The major point is, however, temperature anomalies. And the fact is that temperature anomalies in climate are modeled and predicted much more accurately than absolute temperatures. Competent physicists are well placed to learn any additional background they might need in climate and modeling to understand this point. You could do this too, Peter, rather than side track into disputes over what is “usual” for measurements in general. Get into the specific quantity of interest here — temperature anomalies — and learn about it; that’s the thing for a physicist.
I must confess that I am having difficulty in understanding what this anomaly truly represents, given that the sample set is constantly changing over time.
If the sample set were to remain true and the same throughout the time series, then it would be possible to have an anomaly across that data set, but that is not what is or has happened with the time series land based thermometer data set.
The sample set of data used in say 1880 is not the same sample set used in 1900 which in turn is not the same sample set used in 1920, which in turn is not the same sample set used in 1940, which in turn is not the same sample set used in 1960, which in turn is not the same sample set used in 1980, which in turn is not the same sample set used in 2000, which in turn is not the same sample set used in 2016.
You mention the climatology reference of 1981 to 2010 against which the anomaly is assessed, however, the data source that constitutes the sample set for the period 1981 to 2010, is not the same sample set used to ascertain the 1880 or 1920 or 1940 ‘data’. We do not know whether any calculated anomaly is no more than a variation in the sample set, as opposed to a true and real variation from that set.
When the sample set is constantly changing over time, any comparison becomes meaningless. For example, if I wanted to assess whether the average height of Americans has changed over time, I cannot ascertain this by say using the statistic of 200 American men measured in 1920 and finding the average, then using the statistics of 200 Finnish men who speak English measured in 1940 and finding the average, then using the statistics of 100 American women and 100 Spanish men who speak English as measured in 1960 etc. etc
It is not even as if we can claim that the sample set is representative since we all know that there is all but no data of the Southern hemisphere going back to say 1880 or 1900. In fact, there are relative few stations that have continuous records going back 60 years, still less about 140 years. Maybe it is possible to do something with the Northern Hemisphere, particularly the United States which is well sampled and which possesses historic data, but outside that, I do not see how any meaningful comparisons can be made.
Your further thoughts would be welcome.
No one is talking about any procedure with the built in biases you envision. Not even close. Professionals studying climate really aren’t going to make such incompetent errors. Or, should one do so, others will catch the error quickly.
Coverage is sufficient to get good global estimates back to 1880. This includes the BEST team which made an argument related to what you’re suggesting though not nearly so extreme. This figure shows their value estimates and estimates of the associated errors going back to 1750. Note the error bars are quite acceptable relative to the signal back to 1880 but start growing very fast prior to that time.
http://berkeleyearth.org/wp-content/uploads/2015/02/decadal-comparison-small.png
This may be a bit pedantic, but I take issue with the claim “[R]eanalyses are effectively the weather forecasts you would have got over the years if we had modern computers and models available”. “Analyses” are essentially weather maps, which are (basically) subsets of the model initial conditions from which a forecast can be made–i.e., analyses are not themselves forecasts. Roughly speaking, the initial condition at a given time (let’s call it T) is derived by combining current observations with the previous forecast (started from the initial condition valid at time T-1). I am glossing over a lot of subtleties of the algorithms used to do this, including e.g. how observations collected at several different times can be used to prepare an analysis. For those interested in learning more at a not-too-technical level, Paul Edwards’s book “A Vast Machine” has what appears to me to be a good chapter about this.
Communicating with journalists and the public via the anomaly from a reference period is not accomplishing the goal of highlighting man’s impact on the climate. Even during the reference period, the trend in mean temperature was changing. If the temperature forcings during the reference period are still present in the reporting period, then the overall anomaly from a reference period combines all sources for change, not just man’s impact. Would it not be better to report the change in the rate of the anomaly from the reference period? This would highlight the actual effect of policy change over time.
Can I ask a perhaps silly question regarding anomalies.
Picture you have 3 stations fairly close together. They measure max temps of 88F, 90F, 92F. Further away there is another station measuring max temp of 60F. What is the corectly recorded max temp for this area?
A. 92
B. 88+90+92 / 3 = 90
C. 88+90+92+60 / 4 = 82.5
If we assume C is right. Next year we measure
90+92+94+62 / 4 = 84.75. We now have a trend of 84.75-82.5 = +2.25F
With anomalies let’s assume the following baseline 90,90,90 and 58.
First reading is than:
(-2+0+2+2) / 4 = 0.25
Second reading is:
(0+2+4+4) / 4 = 2.5
We have the very same trend 2.5-0.25 = +2.25F
I do understand anomalies can be used to guess a station’s value if a reading is missing. But I don’t understand how/if anomalies are better than actual temps when selecting A, B or C above.
Dear moderator can you please use this instead.
Can I ask a perhaps silly question regarding anomalies.
Picture you have 3 stations fairly close together. They measure max temps of 88F, 90F, 92F. Further away there is another station measuring max temp of 60F. What is the corectly recorded max temp for this area?
A. 92
B. 88+90+92 / 3 = 90
C. 88+90+92+60 / 4 = 82.5
If we assume C is right. Next year we measure
90+92+94+62 / 4 = 84.5. We now have a trend of 84.5-82.5 = +2F
With anomalies let’s assume the following baseline 90,90,90 and 58.
First reading is than:
(-2+0+2+2) / 4 = 0.5
Second reading is:
(0+2+4+4) / 4 = 2.5
We have the very same trend 2.5-0.5 = +2F
I do understand anomalies can be used to guess a station’s value if a reading is missing. But I don’t understand how/if anomalies are better than actual temps when selecting A, B or C above
When you are studying warming or cooling, the focus is, well, on warming/cooling. Therefore, it is common statistical practice to subtract the mean differences of individual stations out. The mean differences are irrelevant and get at no larger point.
Reduced to 2 stations over 2 years, this this would work as follows:
Station A: 25C 27C
Station B: 15C 16C
Now we can talk about the trend as “actually” going from 20C to 21.5C but that value is meaningless and indeed can add confusion. It certainly isn’t any “actual” global mean surface temperature (whatever global mean surface temperature even means in practice). The key “actual” point to be communicated is that the system has changed by an average of 1.5C over the 2 stations.
This sort of thing is done in many areas where you analyze time series.
Matz asks: Can I ask a perhaps silly question regarding anomalies.
Picture you have 3 stations fairly close together. They measure max temps of 88F, 90F, 92F. Further away there is another station measuring max temp of 60F. What is the corectly recorded max temp for this area?
Matz, the answer is “none of the above”. The problem is in even thinking in terms of “max temp for an area”. There are substantial differences in microclimate even over small areas, so when obtaining a “max temp” you do it at a location. Not an area.
(You can, of course, identify the hottest locations. It is averaging the locations to give a temperature for an “area” that should be avoided.)
What anomalies do is treat each station separately. For each individual station, you look at what is normal, or baseline, for that location. You do this without reference to any of the other stations. Then you identify variations from the baseline at that location. This is the anomaly.
Then you can start to look at the anomalies of the four stations. They should be pretty similar. You can average the anomaly (not and never the temperature) to get the anomaly for the area.
At no point do you ever calculate or consider an average temperature in an area. You only ever look at anomalies for an area.
It is also by comparing the anomalies that you identify any issues with measurement, and deal with an adjustments. Several ways of doing this, but as far as I know all such methods work by comparing anomalies.
Bottom line. Don’t even think about the temperature over an area. It’s not a well defined or particularly useful quantity.
Thanks Chris for you prompt answer.
Maybe I am thick here but the anomaly is just temp minus an offset.
This offset should be the baseline period average temperature for the station, yes. But could be -100 or even the price of your car, it does not matter.
The trend will always be the same if you compare the anomaly with anomaly+the selected offset. Mathematically there is no differens in averaging temps or anomalies.
So we agree anomaly is good to verify that a station reading is within expected range or as infill for missing readings or for interpolation among neighboring stations.
For presentation anomaly alone is misleading because it masks the reason for the trend.
#29 Chris Ho-Stuart:
“There are many situations in which it is best to measure all kinds of quantities as differences, not as absolute values.”
I don’t understand this. If you want to measure the length of a table you measure the length of the table. This is not a difference but the length of an object.
[Response: You miss the point I think. I could measure the absolute position of both ends of the table and take a difference, or just measure the delta of one end to another. As you note the latter is the better option. – gavin]
Just an observation about education, educating the public, and so on.
Several people, including Gavin, have given explanations which appear to me, and I assume others, to be very well crafted. But there are still people “not getting it”.
The problem is that the “teacher” in this kind of situation has no information about the “student”. It doesn’t matter how clear or clever the wording; if it isn’t tailored to where the student is in knowledge and experience, it will accomplish nothing– the key and the lock have to match.
This is not a criticism but a suggestion to both, particularly the “student”: You have to be willing to engage in a process, rather than giving up or simply repeating yourself. (Assuming you are sincere in wanting to understand.)
And it would be courteous at least, if you do “get it” thanks to the explanation from the moderator or other commenters, to acknowledge and demonstrate your enlightenment.
zebra:
Timely and well-put, z. In my own expereience, an AGW-denier’s knowledge and experience are often evident in his comments, even if his motives for denial aren’t. “Reasoning will never make a Man correct an ill Opinion, which by Reasoning he never acquired” (Swift), but brief, well-crafted basic rebuttals of easily exposed AGW-denier memes may help the hypothetical ‘lurker’.
More detailed arguments can be linked from other sites, like those in RC’s lower right-hand list. Linking to a cartoon can save 1,000 words at mininum. Referring educated non-specialists to Weart’s The Discovery of Global Warming is always appropriate, as a source that clearly has no political agenda.