Most of the images showing the transient changes in global mean temperatures (GMT) over the 20th Century and projections out to the 21st C, show temperature anomalies. An anomaly is the change in temperature relative to a baseline which usually the pre-industrial period, or a more recent climatology (1951-1980, or 1980-1999 etc.). With very few exceptions the changes are almost never shown in terms of absolute temperatures. So why is that?
There are two main reasons. First of all, the observed changes in global mean temperatures are more easily calculated in terms of anomalies (since anomalies have much greater spatial correlation than absolute temperatures). The details are described in the previous link, but the basic issue is that temperature anomalies have a much greater correlation scale (100’s of miles) than absolute temperatures – i.e. if the monthly anomaly in upstate New York is a 2ºC, that is a good estimate for the anomaly from Ohio to Maine, and from Quebec to Maryland, while the absolute temperature would vary far more. That means you need fewer data points to make a good estimate of the global value. The 2![]() uncertainty in the global mean anomaly on a yearly basis are (with the current network of stations) is around 0.1ºC in contrast that to the estimated uncertainty in the absolute temperature of about 0.5ºC (Jones et al, 1999).
uncertainty in the global mean anomaly on a yearly basis are (with the current network of stations) is around 0.1ºC in contrast that to the estimated uncertainty in the absolute temperature of about 0.5ºC (Jones et al, 1999).
As an aside, people are often confused by the ‘baseline period’ for the anomalies. In general, the baseline is irrelevant to the long-term trends in the temperatures since it just moves the zero line up and down, without changing the shape of the curve. Because of recent warming, baselines closer to the present will have smaller anomalies (i.e. an anomaly based on the 1981-2010 climatology period will have more negative values than the same data aligned to the 1951-1980 period which will have smaller values than those aligned to 1851-1880 etc.). While the baselines must be coherent if you are comparing values from different datasets, the trends are unchanged by the baseline.
Second, the absolute value of the global mean temperature in a free-running coupled climate model is an emergent property of the simulation. It therefore has a spread of values across the multi-model ensemble. Showing the models’ anomalies then makes the coherence of the transient responses clearer. However, the variations in the averages of the model GMT values are quite wide, and indeed, are larger than the changes seen over the last century, and so whether this matters needs to be assessed.
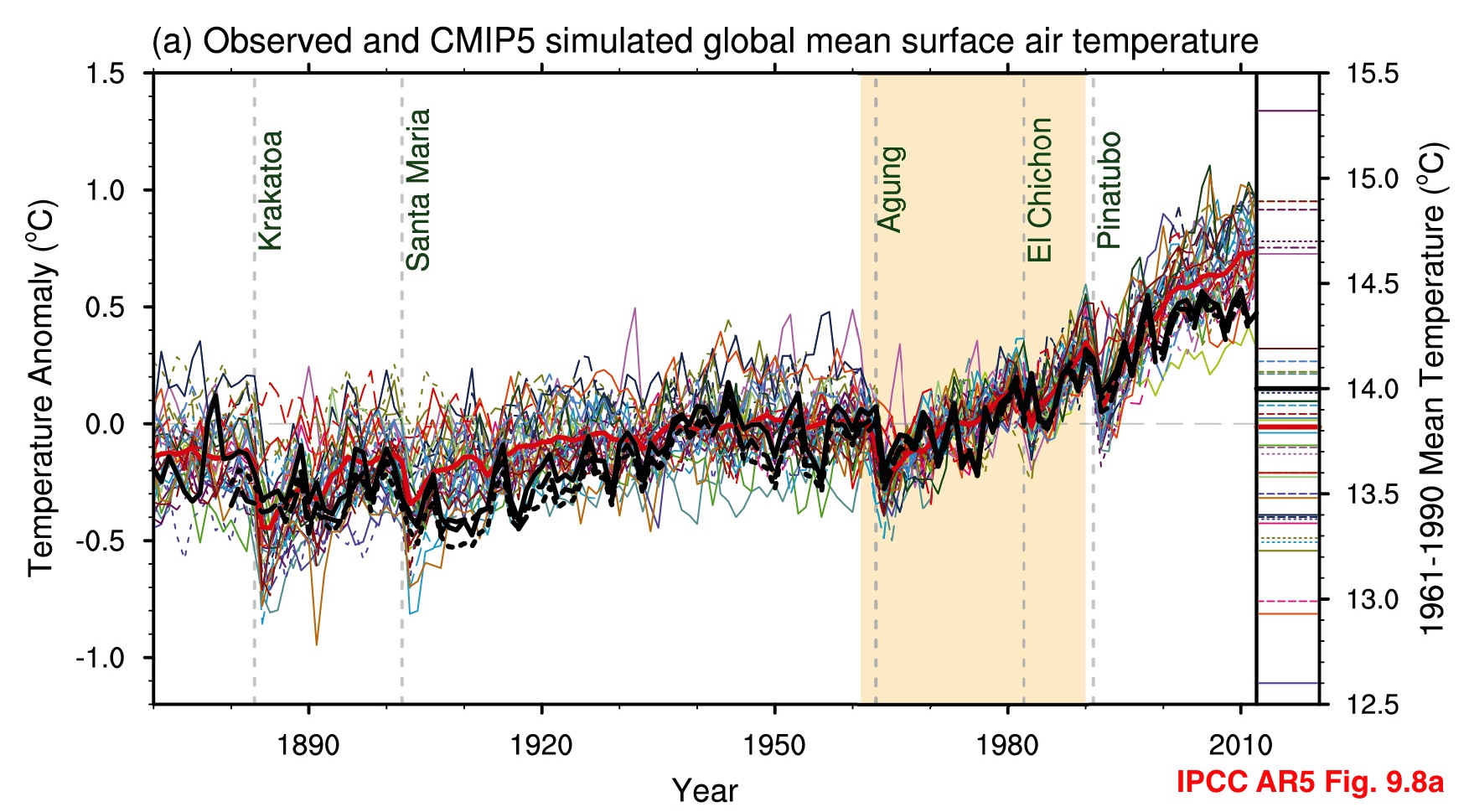
IPCC figure showing both anomalies as a function of time (left) and the absolute temperature in each model for the baseline (right)
Most scientific discussions implicitly assume that these differences aren’t important i.e. the changes in temperature are robust to errors in the base GMT value, which is true, and perhaps more importantly, are focussed on the change of temperature anyway, since that is what impacts will be tied to. To be clear, no particular absolute global temperature provides a risk to society, it is the change in temperature compared to what we’ve been used to that matters.
To get an idea of why this is, we can start with the simplest 1D energy balance equilibrium climate model:

In the illustrated example, with S=240 W/m2 and =0.769, you get a ground temperature (
) of 288 K (~15ºC). For the sake of argument, let’s assume that is the ‘truth’. If you (inaccurately) estimate that
= 0.73, you get
=286K – an offset (error) of about 2K. What does that imply for the temperature sensitivity to a forcing? For a forcing of 4 W/m2 (roughly equivalent to doubling CO2), the change in
in the two cases (assuming no feedbacks) is an almost identical 1.2 K. So in this case, the sensitivity of the system is clearly not significantly dependent to small changes in GMT. Including a temperature feedback on
would change the climate sensitivity, but doesn’t much change the impact of a small offset in
. [Actually, I think this result can be derived quite generally based just on the idea that climate responses are dominated by the
Planck response while errors in feedbacks have linear impacts on
].

We can also broaden this out over the whole CMIP5 ensemble. The next figure shows that the long term trends in temperature under the same scenario (in this case RCP45) are not simply correlated to the mean global temperature, and so, unsurprisingly, looking at the future trends from only the models that do well on the absolute mean doesn’t change very much:


A) Correlation of absolute temperatures with trends in the future across the CMIP5 ensemble. Different colors are for different ensemble members (red is #1, blue is #2, etc.). B) Distribution of trends to 2070 based on different subsets of the models segregated by absolute temperatures or 20th Century trends.
So, small (a degree or so) variations in the global mean don’t impact the global sensitivity in either toy models, single GCMs or the multi-model ensemble. But since there are reasonable estimates of the real world GMT, it is a fair enough question to ask why the models have more spread than the observational uncertainty.
As mentioned above, the main problem is that the global mean temperature is very much an emergent property. That means that it is a function of almost all the different aspects of the model (radiation, fluxes, ocean physics, clouds etc.), and any specific discrepancy is not obviously tied to any one cause. Indeed, since there are many feedbacks in the system, a small error somewhere can produce large effects somewhere else. When developing a model then, it is far more useful to focus on errors in more specific sub-systems where further analysis might lead to improvements in that specific process (which might also have a knock on effect on temperatures). There is also an issue of practicality – knowing what the equilibrium temperature of a coupled model will be takes hundreds of simulated years of “spin-up”, which can take months of real time to compute. Looking at errors in cloud physics, or boundary layer mixing or ice albedo can be done using atmosphere-only simulations which take less than a day to run. It is therefore perhaps inevitable that the bounds of ‘acceptable’ mean temperatures in models is broader than the observational accuracy.
However, while we can conclude that using anomalies in global mean temperature is reasonable, that conclusion does not necessarily follow for more regional temperature diagnostics or for different variables. For instance, working in anomalies is not as useful for metrics that are bounded, like rainfall. Imagine that models on average overestimate rainfall in an arid part of the world. Perhaps they have 0.5 mm/day on average where the real world has 0.3 mm/day. In the projections, the models suggest that the the rainfall decreases by 0.4 mm/day – but if that anomaly was naively applied to the real world, you’d end up with an (obviously wrong) prediction of negative rainfall. Similar problems can arise with sea ice extent changes.
Another problem arises if people try and combine the (uncertain) absolute values with the (less uncertain) anomalies to create a seemingly precise absolute temperature time series. Recently a WMO press release seemed to suggest that the 2014 temperatures were 14.00ºC plus the 0.57ºC anomaly. Given the different uncertainties though, adding these two numbers is misleading – since the errors on 14.57ºC would be ±0.5ºC as well, making a bit of a mockery of the last couple of significant figures.
So to conclude, it is not a priori obvious that looking at anomalies in general is sensible. But the evidence across a range of models shows that this is reasonable for the global mean temperatures and their projections. For different metrics, more care may need to be taken.
References
- P.D. Jones, M. New, D.E. Parker, S. Martin, and I.G. Rigor, "Surface air temperature and its changes over the past 150 years", Reviews of Geophysics, vol. 37, pp. 173-199, 1999. http://dx.doi.org/10.1029/1999RG900002
Link to 3rd graphic broken for me at least.
[Response: Fixed. thanks – gavin]
Are there specific places where getting the absolute temperature right is more of an issue for models? I’m thinking e.g. of ice, where one degree above or below zero may make a relatively large difference. Is this a significant question and are there other examples? Thanks.
The term toy model is a good one.
If you would like my update to a toy model similar to the one in the link, I’ll be glad to send it.
In answer to JK, would that it were so one dimensional, for sea ice you also have to get the salinity of the water underneath the ice, which is a dynamic quantity. The freezing point of salt water varies strongly with the salinity which changes as the ice underneath melts and freshens the sea.
I think another reason for using anomalies is that they don’t have a big spread in expected value, so you can compare averages at different times without worrying too much about missing values. One should worry enough, as Cowtan and Way showed. But when NOAA do a absolute temperature average for CONUS (before recent change), they have to keep exactly the same stations, interpolating missing values. Dependence on the goodness of interpolation is much higher.
Ok, the models have done a pretty good job of estimating global temperature anomalies. And, it is nice to be able to give the modelers kudos for a win. (We were not so sure, running card decks in the basement of NCAR in 1964.) However, are GLOBAL temperature anomalies useful in the real world? Did they warn us of the 2007 Arctic sea ice retreat? Did it warn us of the ongoing Antarctic glacier (PIG) bottom melt? All of the real impacts and effects of AGW are local events – weather as it were. People have died in heat waves affected by AGW. However, those people died from the local temperature, and not the average global temperature.
If modelers are going to focus on GLOBAL temperature anomalies, then we need a set of conversion factors that allow planners to map from predicted global temperature anomalies to a local basis of engineering, risk assessment, and planning.
In my culture, the most learned men debated, “How many angels can dance on the head of a pin?” for centuries. I have come to see modeling global temperature anomalies as a similar pastime. Modeling global temperature anomalies is just a way of delaying answering the real questions of how local conditions will affect the people and infrastructure at that location.
I understand the resource issues, but perhaps the lack of useful product indicates that we should be considering modeling options rather than explaining and apologizing for a class of models that seem to have plateaued without yielding very useful results I suggest that our (good) community climate models have hindered our search for better climate models.
And regarding #4, pressure is also important for the melting point of fresh water ice, but less so for salt water ice (e.g., anchor ice.) Thus, the PIG melts from the bottom up. In the real world, effects of AGW are so localized that the top and bottom of the same glacier melt at different rates. With any averaging, this melt that changes the grounding line and hence the rate of flow is lost and the model fails to correctly estimate ice flow.
With reference to the “simple Energy Balance Model”;
Why is there no arrow showing the reflection of the incoming insolation at the boundary with Ta?
Surely if the Earths radiation is reflected back to Earth from that boundary (shown as a dotted line, Ta), then some of the incoming energy (in the band reflected at Ta) will also be reflected back to the sky?
The amount reflected will also be modulated by the density of the “greenhouse gas layer” as depicted in this simple diagram.
The result being that as the “greenhouse gas layer reflection increases, so less energy (in the appropriate frequency band, or bands) will reach the Earth, compensating for the increased “greenhouse effect”
Please explain……
[Response: The reflection is absorbed into the definition of S (which is the averaged solar flux minus the reflected portion). Since GHGs are (mostly) transparent to visible and near-IR light this makes little difference and simplifies the model a lot. Note that this model is just pedagagoical – not an accurate model of the real world. – gavin]
In Chapter 9 of the latest IPCC report, I read that “The global mean fraction of clouds that can be detected with confidence from satellites (optical thickness >1.3) is underestimated by 5 to 10 %. Some of the above errors in clouds compensate to provide the global mean balance in radiation required by model tuning.” As I interpreted those two sentences, the models were adjusted to produce an absolute global mean temperature in agreement with the measurements over the past century. Since apparently there is not agreement in absolute temperature, would someone please explain what those two sentences actually meant?
If the models incorrectly calculate the absolute cloud coverage, then isn’t it also reasonable to guess that the models will incorrectly calculate any changes in cloud coverage? Stated another way, since the cloud coverage is in some sense a feedback from the warming due to carbon dioxide, wouldn’t a change in carbon dioxide also lead to an incorrect change in the feedback of cloud formation?
The reluctance of GISTEMP to follow HADCRUT and publish offsets for monthly data rather than just an offset for the annual data might be overcome by publishing monthly offsets relative to the annual figure. These would have high precision compared to the uncertainty in the absolute number for annual data. And it would help to avoid confusion that leads to false claims such as January 2007, with its 0.92 C anomaly, being the hottest month ever when it really very unlikely, owing to the lager seasonal amplitude of the Northern hemisphere, for January to ever be the hottest month overall. http://data.giss.nasa.gov/gistemp/tabledata_v3/GLB.Ts+dSST.txt
I should be clearer. GISTEMP is published intentionally leaving out a table of monthly offsets that would correspond to fig. 7. in the cited paper by Jones et al. (1999) which provides information that allows clearer interpretation of HADCRUT data. It is obvious from fig. 7. that the month-to-month climatology is not afflicted by 0.5 C relative error and this is more a systematic uncertainty shifting the whole curve. GISTEMP could make this explicit by publishing the same information relative to zero rather than relative to 14.0 C.
Gavin,
I’m a bit cross with myself right now for my naive assumptions about the relationship between absolute and anomalized GCM GMT output, for I have previously lead myself to some wrong conclusions. Last night I retired having generated this plot from CMIP5 RCP4.5:
https://drive.google.com/file/d/0B1C2T0pQeiaSSGFhdjlnd3hkX0U/view
You say in your article, “To be clear, no particular absolute global temperature provides a risk to society, it is the change in temperature compared to what we’ve been used to that matters,” which I long ago internalized because I find it quite sensible. On that score I have known for some time by my own investigation of CMIP5 GMT anomaly output that GCMs do a remarkable job of agreeing with each other, which inspires confidence.
Then you say, “But since there are reasonable estimates of the real world GMT, it is a fair enough question to ask why the models have more spread than the observational uncertainty.” Prior to yesterday the fairness of that question lacked context for me. Today what I know is that for HADCRUT4GL, the published error ranges for monthly data are: min 0.21 K, max 1.38 K, mean 0.44 K.
For the CMIP5 RCP4.5 ensemble monthly absolute GMT, from 1861-2014, monthly spreads are: min 3.04 K, max 3.75 K, mean 3.37 K.
You begin your last graf with, “So to conclude, it is not a priori obvious that looking at anomalies in general is sensible.” Two days ago I would not have thought that such a masterful exercise in dry understatement. I get it that you do this stuff for a living, but the figures I list above are fresh news to me. Being that I’m somewhat shocked, please bear with me. The crux of this for me is your final statement, “For different metrics, more care may need to be taken.”
I emphatically agree, and that’s me exercising dry understatement. Let me attempt to focus this rant into a constructive question or two. Where can an avid but amateur hobbyist such as me go to get my mind around what due care has been taken for other metrics, either global or regional? A concise list of other metrics would be a good start, but I’m particularly interested in precipitation and ice sheets. If you don’t think those two are the most particularly interesting, what two or three metrics top your list as the most critically uncertain?
[Response: Surface mass balance on the ice sheets is a good example. As are regional rainfall anomalies, sea ice extent changes etc. Basically anywhere where there is a local threshold for something. Most detailed analyses of these kinds of things do try to assess the implications for errors in the climatology, but it is often a little ad hoc and methods vary a lot. – gavin]
I would like to see a paper that proves scientifically or statistically or mathematically this point:
“The 2\sigma uncertainty in the global mean anomaly on a yearly basis are (with the current network of stations) is around 0.1ºC in contrast that to the estimated uncertainty in the absolute temperature of about 0.5ºC (Jones et al, 1999).”
Proves as in shows that this is physically true and not just true in the sense that a statistician would call true. In other words, is it physically true that the anomaly is closer to the ACTUAL PHYSICAL truth, or it is just conveniently “truer” in a stats sense?
[Response: If we knew the absolute truth, we would use that instead of any estimates. So, your question seems a little difficult to answer in the real world. How do you know what the error on anything is if this is what you require? In reality, we model the errors – most usually these days with some kind of monte carlo simulation that takes into account all known sources of uncertainty. But there is always the possibility of unknown sources of error, but methods for accounting for those are somewhat unclear. The best paper on these issues is Morice et al (2012) and references therein. The Berkeley Earth discussion on this is also useful. – gavin]
Aaron Lewis writes, “People have died in heat waves affected by AGW.” In discussions of climate change, reports of deaths caused by temperature extremes are highly misleading if only deaths caused by excessively warm temperatures are cited. In a 2014 CDC paper, J. Berko, et al, reported that of deaths in the US attributed to weather, 31 percent resulted from excessive heat and related effects while 63 percent resulted from excessive cold and related effects. (Deaths Attributed to Heat, Cold, and Other Weather. Events in the United States, 2006–2010, http://www.cdc.gov/nchs/data/nhsr/nhsr076.pdf.)
In short, from 2006 to 2010 more than twice as many people died from the effects of excessive cold than excessive heat.
[Response: You are confusing winter deaths with deaths from cold itself. The relationship is not that direct – see Ebi and Mills (2013) for a more complete assessment. – gavin]
Concerning comment (3) from Rob Quayle: Yes, I am interested in the updated
toy model. Could you send me it to ansar@matcuer.unam.mx ? Thanks
To be clear, no particular absolute global temperature provides a risk to society, it is the change in temperature compared to what we’ve been used to that matters.
Clarity meets Climate Change, with this takeaway message: get used to it.
As I understand all models they all predict a water vapour based forcing caused by increased temperatures leading to increased levels of water vapour and hence an increased greenhouse effect.
Would a higher or indeed lower absolute mean global temperature now affect this forcing as temperature increased due to CO2 in the future or is the effect minimal. It seems to me it may be significant given that the capacity of air to hold moisture increases at a faster than linear rate.
[Response: For anything near present temperatures, WV increases at roughly 7% per ºC and the feedback is tied to this – hence the size of the feedback doesn’t vary a lot the absolute global mean temperature. – gavin ]
“roughly equivalent to doubling CO>sub>2” has a typesetting error.
Imo, the baselines used in the anomaly series create an additional source of confusion that’s totally unnecessary wrt to the ‘limits above preindustrial temperatures’. Anyone looking at the series can quickly come to a conclusion that there’s still plenty of room for the temperature increase as the zero-point in these has been chosen not to be the preindustrial but the base period. Maybe this works as an initiation ceremony for students who, when they actually calculate how far off natural the globe really is, but for even somewhat innumerate less scientific public this is a hurdle that’s not very easily taken. There is of course the scientific reason to measure the anomalies against the most accurate baseline period, but as for educating the public, I’m not too sure they do more benefit than harm. In order to do your own calculations (likely not as scientific as the real scientists), you have to build temperature series of your own that would have f.e. latitudinal bands of the freezing point of water, which is pretty relevant info for everyday applications. meh.
In the paragraph before the last one, there’s one “the” too many: “making the a bit of a mockery of the last couple of significant figures.”
When I look up the temperature anomalies relative to the base period 1951-1980 for Nov 2014 at http://data.giss.nasa.gov/gistemp I find a change of 0.65 °C for GLB.Ts+dSST.txt and 0.78 °C for NH.Ts+dSST.txt . As I am living on the Northern hemisphere on land I also looked up NH.Ts.txt : 1.00 °C. To be more precise I also looked up the gridded data file for the segment 10 E-15 E, 45 N-50 N: 2.70 °C. To compare this with local weather stations I find for Germany 4.1 °C for the base period and 6.5 °C for Nov 2014, i. e. a temperature anomaly of 2.4 °C, same for Munich 4.0 °C for the base period and 6.4 °C for Nov 2014, i.e. a temperature anomaly of 2.4 °C. In order to estimate the UHI effect I also looked up the relevant temperatures for HohenPeissenberg a nearby rural weather station: 2.4 °C for the base period 1951-1980 and 6.4 °C for Nov 2014, i.e. a temperature anomaly of 4.0 °C. This seems to be an anti UHI effect. Conclusions: When you go local things are getting complicated and you should better use temperatures instead of anomalies for your plans.
Gavin,
Very nice and informative post.
I have once before seen a plot of global mean temperature against modeled future temperature increases. While noisy, the correlation looks significant, with those models that calculate a warmer mean temperature projecting (on average) a lower rate of future warming. Do you have any idea why this would be? Do you think knowledge of “absolute truth” global average temperature would help to evaluate which model projections are closer to reality?
Happy holidays to you and yours.
Kip Hansen: “Proves as in shows that this is physically true and not just true in the sense that a statistician would call true. In other words, is it physically true that the anomaly is closer to the ACTUAL PHYSICAL truth, or it is just conveniently “truer” in a stats sense? – See more at: https://www.realclimate.org/index.php/archives/2014/12/absolute-temperatures-and-relative-anomalies/comment-page-1/#comment-621675
What the hell does this even mean?
> Kip Hansen: … the ACTUAL PHYSICAL truth
As has been remarked about politics, eh?
All truth is local. For statistics, you need samples of a population.
Steve Fitzpatrick says:
Yes, I have seen global mean temperature plotted against modeled future temperature increases many times.
No, you don’t seem to understand that warmer calculated temperatures imply higher rate of warming. That is pretty intuitive.
try again.
WHT,
Maybe you misunderstand what I was asking. I was referring to the plot of absolute average surface temperatures from different models against the projected rate of warming for 2011 to 2070 from those same models; this is the next to last graphic from Gavin’s post. There appears to be some correlation (though noisy) which might be informative. Perhaps I could hand digitize the data points and see if the OLS slope is significant, based on an F-test.
I digitized Gavin’s next to last graphic using “PlotDigitizer”. I switched the X and Y axis and calculated the OLS trend line. Here is the result: http://i57.tinypic.com/fnbs69.png
The R^2 value is relatively low (noisy). The F statistic is 26 (78 degrees of freedom). What I find most interesting is that the models are not normally distributed in calculated average surface temperature; there is a relatively tight cluster of models (22 data points) around 14.7 +/- 0.15C absolute temperature and the rest spread out over 12.3C to 14.1C; perhaps the clustered models are based on common assumptions an/or strategies which lead to a relatively consistent calculated average surface temperature.
First of all, if you are going to look at the future trends as a function of absolute mean, you need to switch the axes of the scatter plot. As it is, it is more difficult to interpret the details for various values of global means. Despite this, it is fairly evident that there is a negative relationship between the two variables. Perhaps you could actually calculate the value of the correlation coefficient to indicate the strength of the relationship (and possibly provide a p-value for the result).
Secondly, the graph of the densities is incomplete and somewhat misleading. The curves for “all models” and “13.5 less than GMST less than 14.5” both range over the entire width of the graph. But where is the information for those models whose values are outside of the latter interval? In particular, since there appears to be a relationship between the two variables, this information should be given separately for those models with GMST is above 14.5 and those which are below 13.5. I suspect there would be very little overlap of the two densities.
Finally, because of the posited strong water vapor feedback, which depends on absolute, not anomaly, temperatures, one would expect that the relationship should be positive, not negative due to the greater rate of accumulation of water vapor at higher absolute temperatures. This does not appear to be the case for these models.
Your criticism of the WMO press release seems a little churlish. Sure, the two decimal places on the 14°C are ridiculous, but if the best way to estimate change is by appropriate averaging of anomalies, then the best way to estimate changed absolute must be to apply the averaged anomaly to some adopted value of the pre-change absolute. The 14°C (without the decimals) seems a decent pick for that. Yes it’s highly uncertain, but that uncertainty is irrelevant to discussion of change and can fairly be ignored, I think … at least in a press release.
Given a spatially and temporally sparse set of point measurements of the behavior of a complex but well understood system, the best way to estimate the overall system behavior is arguably to build a robust model of its physics and train that over time to reproduce the measurement field. Such data assimilation modeling is, for example, how PIOMAS works. Why is this approach not much used for estimating global mean surface temperature change? Apparently suitable reanalysis models have existed for decades, and the latest (e.g. ERA-interim) appear to be seriously good. The need to fuss about anomalies vs absolutes then magically vanishes, as do those data holes.
Hi Roman,
See my comment #26, which I believe does the things you suggest. The P value is <0.001, if I have read the F table correctly.
WRT water vapor amplification, I suspect that the basic (radiative only) amplifying effect of water vapor, which is something less than a factor of 2 over the CO2-only effect of ~1.2C, IIRC, will be close to the same across a range of average surface temperatures. The (apparent) slower rate of projected model warming for a higher absolute temperature may be related to other factors like cloud amount and geographical distribution at higher absolute humidity, or increases in convective transport (due to more atmospheric instability) at higher absolute humidity.
The puzzle for me is why some models are tightly clustered around 14.7C average temperature, and others spread over a fairly wide (and lower) temperature range. It would be interesting to know which models form the cluster near 14.7C. Maybe Gavin knows this.
[Response: There are a couple of issues here – first, the number of ensemble members for each model is not the same and since each additional ensemble member is not independent (they have basically the same climatological mean), you have to be very careful with estimating true degrees of freedom. You can ameliorate this a little by only selecting a single ensemble member from each model (e.g. only the red dots, or only blue dots, or randomly selecting from each ensemble etc.) before doing any analysis. But even that isn’t really enough, because some of the models are closely related to each other (i.e. ACCESS and HadGEM2, or any of the GISS models). Furthermore, different model groups have different strategies for calibration of their simulations and that could cause some grouping. The models around 14.7ºC are MIROC5, BCC and five flavours of the GISS model. Anything beyond histograms (e.g. significance of trends etc.) needs to deal with this somehow and it gets complicated fast. – gavin]
#6 Aaron Lewis
Microclimate seems to be a subject in need much modeling. Now that AGW and climate change are settled and have been for quite a while, it would seem prudent to find oases of habitable territory in otherwise inhospitable areas. New modeling techniques might be valuable in such searches as these areas will certainly change, but not in lockstep with the expected broader climate changes.
http://en.wikipedia.org/wiki/Microclimate
#30 Steve Fitzpatrick
Yes, my comment was suggesting exactly what you did. When I posted it, your comment was not visible even though the time stamp was four and a half hours earlier – probably due to some delay in moderation.
From the statistics that you calculated, the correlation coefficient for the two variables is close to .501. Noting that the F distribution with 1 and 78 degrees of freedom is the distribution of the square of a t-variable with 78 df, the two-sided p-value is of the order of 2E-6. Some of the strength of that relationship, but not all, is indeed due to the cluster of models with GMST greater than 14.5.
My point with the water vapor was based on the fact that the maximum amount appears to increase as a percentage of the current maximum thereby allowing for rates of temperature increase somewhat greater than linear at higher temperatures. Of course, this effect can be moderated by other factors if those factors are treated differently by the various models.
Another question which has occurred to me as well is whether there is a substantial difference between models in frequency and intensity of hurricanes. It is my understanding that the formation of hurricanes is largely dependent on the presence of a baseline minimum (absolute) temperature. If the GMSTs differ by as much as 2 or 3 degrees, how much do model SSTs in hurricane formation regions differ? I would be curious to learn that.
Since the usual suspects have already fielded a flatline graph of recent global temperature in Kelvins – it’s still 293 out there give or take a degree, it’s only one small Dunning -Kruger step before Watts, Morano, the Bishop and Bast. point triumphantly to the cosmic microwave background temperature of the last century and declarethat warming impossible on the grounds that it’s only 4.6 Kelvin in all directions as far as you can look.
Hi Roman,
I do not think climate models have nearly small enough grid scale to accurately model hurricane formation, although they apparently do show some (weaker) vortex formation. This article may be of interest: http://www.willisresearchnetwork.com/assets/templates/wrn/files/Done_TCs_in_GCMs.pdf
WRT water vapor influence, you are probably right that there is a modest net increase in water vapor amplification at higher average temperature. Modtran indicates that maintaining constant clear sky upward flux after a doubling of CO2 (70 KM altitude, looking down, constant relative humidity) requires ~1.9C higher surface temperature in the tropics but a bit less than 1C in the subarctic. But this is over ~30C temperature difference; over a couple of degrees the difference in the average is going to be pretty small. As you say, other factors are probably more important.
Small typo in comment #32: The correlation coefficient should (obviously) read -.501, not +.501.
Gavin’s caveats in his inline response to comment #30 on measuring and interpreting the strength of the relationship of the GMST and later trend are certainly correct. Accommodating the situation would require information of which specific models and runs were present in the data set used in the head post. A possible starting analytic approach might be a simple Analysis of Covariance to take model families into account.
However, the point I raised earlier on the two groups of models with GMST above 14.5 and GMST below 13.5 still stands. What features of those models produce such drastic differences in the later trends? Has this not already been addressed in some way in the modelling community?
Hi Gavin,
Thanks for your reply. Taking only one run from each model (red points on your graphic) reduces R^2 to 0.1275, and the P value increases to ~0.028. I have no way of knowing the influence of “family relationships” between models, but it is clear that a large part of the apparent correlation of projected warming rate with average surface temperature is due to more runs for some models than for others, combined with the close relationships between certain models. Are these factors taken into account when ensemble estimates are produced (ECS, transient sensitivity, etc.)?
#36 Steve
An Analysis of Covariance (Anacova) is really a regression with different intercepts to accommodate categorical variables. The response variable in this case is the future trend of the model. Estimates of the mean trend are obtained for each family of models (i.e. a set of models coming from the same model team) and at the same time an estimate of the relationship between GSMT and trend is also obtained. This allows for the use of all the model runs.
#34 Steve
With regard to the hurricanes, how can the models predict an increase and measure the rate of that increase if the resolution is insufficient or if the absolute SST is not taken into account?
#37–“…how can the models predict an increase and measure the rate of that increase if the resolution is insufficient or if the absolute SST is not taken into account?”
– See more at: https://www.realclimate.org/index.php/archives/2014/12/absolute-temperatures-and-relative-anomalies/comment-page-1/#comment-622026
I know! I know! (A bit, at least.)
Downscaling approaches, as in this 2003 study. GCM results are used: “The large-scale thermodynamic boundary conditions for the experiments— atmospheric temperature and moisture profiles and SSTs—are derived from nine different Coupled Model Intercomparison Project (CMIP2+) climate models.”
Then a finer-scale model is run to simulate the hurricanes themselves: a “nested regional model that simulates the hurricanes. Approximately 1300 five-day idealized simulations are performed using a higher-resolution version of the GFDL hurricane prediction system (grid spacing as fine as 9 km, with 42 levels).”
http://journals.ametsoc.org/doi/abs/10.1175/1520-0442(2004)017%3C3477:IOCWOS%3E2.0.CO%3B2
Roman (#37),
An analysis of covarience sounds like it might be useful, but you would need to know which models (aside from those Gavin mentioned) are closely related. I don’t. I have not found any references to this in a brief Google search.
#38:
Thanks for the link. The paper does indeed describe how the hurricane modelling is done. I am currently visiting relatives so was only able to scan it briefly, but here are several points I noticed about the paper:
It is somewhat dated since it deals with an earlier generation of models. There has also been substantial new research on the formation of storms. Have there been no improvements in this area since then?
The hurricanes “generated” within the models are all modeled on a single hurricane record from 1996. The evolution of the hurricanes is altered in some way by conditions other than SST (such as humidity) in the various models because the resulting intensity of the hurricanes seems to be shifted somewhat surprisingly by a constant amount across all SSTs according to Figure 11.
There is no information given for the initial characteristics of the individual models although there are graphs for some of the results for each models. Generally averages of all models are used so the variability between them becomes less obvious.
#40–Good questions, and I don’t know the answers. I picked that paper purely as a convenient example of the general strategy I knew to be in use.
If you’d like to search further, I’d use the ‘cited by’ feature in Google Scholar to find out what papers have built on this one. You’d think it’d be a straightforward and quick search–though you never know for sure, I guess. I’d love to hear if you find something interesting.
Happy New Year!
#41:
Maybe I will, but it will have to wait until I get home next week (and if nothing new and more interesting cows along). :)
Happy New Year to the RC Crew and commenters, well, most of you anyway! We appreciate your work and research!
IIRC (which I might not – twas a while ago), in our MIROC ensemble (slab ocean GCM), members with high eqm climate sensitivity also had high control temperature. But I’m not sure this was very meaningful, as it also seemed that with a hot enough control temp, infinite climate sensitivity resulted (ie the model ran away…). I thought it was more likely to be a model building instability than a real world instability…
jules
January’s answer to Groundhog Day is Anthony Watts’ annual attempt to equate the first cold weather anomaly of the new year with the onset of a new Ice Age.
Who needs absolute temperatures? While we wait for their official December values, the NCDC 2014 seasonal year (DEC-NOV) temperature values are complete. The contiguous US is about average, not even in the top 50 warmest years, with the mean temperature about equal to that of the 1949 20th century mean. It is about three degrees lower than in 2012 and has come in at about 0.6°F lower than the 1918 20th century median and seven degrees lower than the 1998 global mean.
RomanM,
Regarding hurricane-like features in models, here is an interesting post by Isaac Held on the subject a few years back: http://www.gfdl.noaa.gov/blog/isaac-held/2011/02/22/2-hurricane-like-vortices/
At the AGU this year there was a lot of neat posters and presentations about the behavior of hurricanes in high-resolution climate models. Higher resolution models tended to get more hurricane formation (perhaps unsurprisingly), with quarter-degree models parameterized using observed SSTs generally capturing historical hurricane formation rates fairly accurately. I recall they still tended to underestimate hurricane strength, however.
Geologist, surely you must have learned during your training to become a geologist that the contiguous United States covers only ~1.5% of Earth’s surface, right?
It’s called global warming/climate change for a reason.
#46–And your point is?
The Japan Meteorological Agency has officially called it:
2014 was by far the hottest year in more than 120 years of record-keeping
The “pause” is dead. Long live the “pause.