… if your data do not look like a quadratic!
This is a post about global sea-level rise, but I put that message up front so that you’ve got it even if you don’t read any further.
The reputable climate-statistics blogger Tamino, who is a professional statistician in real life and has published a couple of posts on this topic, puts it bluntly:
Fitting a quadratic to test for change in the rate of sea-level rise is a fool’s errand.
I’d like to explain why, with the help of a simple example. Imagine your rate of sea-level rise changes over 100 years in the following way:
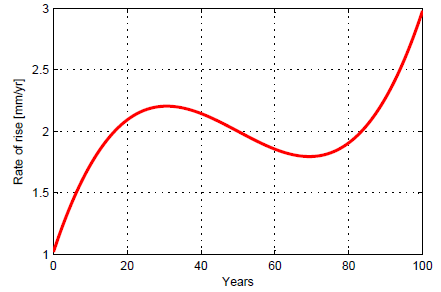
Fig. 1. Rate of sea-level rise as it changes over 100 years. This is a fictitious example chosen for illustrative purposes. It’s simply a polynomial curve, see appended matlab script.
It starts at 1 mm/year, then in the middle of the century it hovers for a while around 2 mm/year (namely between 1.8 and 2.2), and in the end it climbs to 3 mm/year. There can be no question about the fact that the rate of sea-level rise increases overall during those 100 years. It increases by a factor of three, from one to three millimetres per year, although not at a steady rate. You could fit a linear trend to the above curve and also find an increase in the rate – although a linear trend would not be a great description of what is going on, because the increase in rate is clearly not linear. (Note that a linear increase in the rate corresponds to a quadratic sea-level curve.)
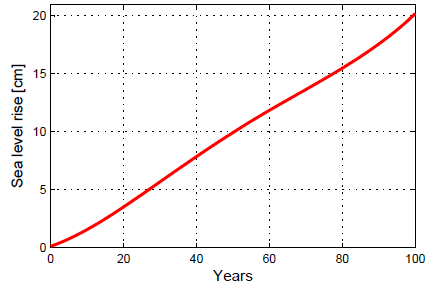
You can easily compute the sea-level curve that follows from the above rate by integrating it over time, and it looks like this:
Fig. 2. This sea level curve is the integral of the curve in Fig. 1 and thus contains the same information, but when viewed in this way it is hard to judge by eye whether sea-level rise has accelerated. The better way to answer this question is by looking at the rate curve, i.e. Fig. 1.
Now here it comes: if you fit a quadratic (by the standard least-squares method) to this sea-level curve, the quadratic term (i.e. the acceleration) is negative! So by this diagnostic, sea level rise supposedly has decelerated, i.e. the rate of rise has slowed down! This clearly is nonsense and misleading (we know the truth in this case, it is shown in Fig. 1), and this nonsense results from trying to fit a quadratic curve to data that do not resemble a quadratic. You can call it a misapplication of curve fitting, or the use of a bad model.
Now to real data
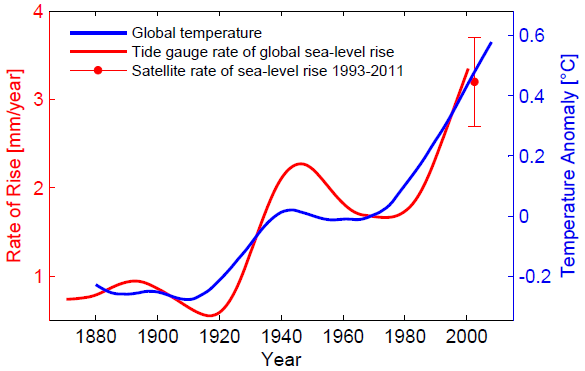
Is this just a bizarre, unrealistic example? No! Because the basic shape of this example resembles the observed global sea-level curve from about 1930 to 2000. The red curve below is the rate of rise as diagnosed from the Church&White (2006) global sea-level data set, as shown and described in more detail in Rahmstorf (Science 2007):
Fig. 3. Rate of global sea-level rise based on the data of Church & White (2006), and global mean temperature data of GISS, both smoothed. The satellite-derived rate of sea-level rise of 3.2 ± 0.5 mm/yr is also shown. The strong similarity of these two curves is at the core of the semi-empirical models of sea-level rise. Graph adapted from Rahmstorf (2007).
Why would it have such a funny shape, with the rate of rise hovering around 2 mm/year in mid-century before starting to increase again after 1980? I think the reason is physics: the warmer it gets, the faster sea-level rises, because for example land ice melts faster. The sea-level rate curve has an uncanny similarity to the GISS global temperature, shown here in blue. The rate of SLR may well have stagnated in mid-century because global temperature also did not rise between about 1940 and 1980, and in the northern hemisphere even dropped.
Houston & Dean
The “sea-level sceptics” paper by Houston and Dean in 2011 claimed that there is no acceleration of global sea-level rise, by doing two things: cherry-picking 1930 as start date and fitting a quadratic. The graphs above show how this could give them their result despite the clear threefold acceleration from 1 to 3 mm/yr during the 20th Century. In our rebuttal published soon after (Rahmstorf and Vermeer 2011), we explained this and concluded:
Houston and Dean’s method of fitting a quadratic and discussing just one number, the acceleration factor, is inadequate.
(There’s quite a few other things wrong with this paper and several responses have been published in the peer-reviewed literature (5? I lost track); we also discussed it at Realclimate.)
So the bottom line is: the quadratic acceleration term is a meaningless diagnostic for the real-life global sea-level curve. Instead, one needs to look at the time evolution of the rate of sea-level rise, as has been done in a number of peer-reviewed papers. For example, Rahmstorf et al. (2012) in their Fig. 6 show the rate curve for the Church&White 2006 and 2011 and the Jevrejeva et al. 2008 sea-level data sets, corrected for land-water storage in order to isolate the climate-driven sea-level rise. In all cases the rate of rise increases over time, albeit with some ups and downs, and recently reaches rates unprecedented in the 20th Century or (for the Jevrejeva data) even since 1700 AD. Similar results have been obtained for regional sea-level on the German North Sea coast (Wahl et al. 2011).
Pitfalls of rate curves
When looking at real data, one needs to be aware of one pitfall: unlike the ideal example shown at the outset, real tide gauge data contain spurious sampling noise due to inadequate spatial coverage, so it is not trivial to derive rates of rise. One needs to apply enough smoothing (as in Fig. 3 above) to remove this noise, otherwise the computed rates of rise are dominated by sampling noise and have little to do with real changes in the rate of global sea-level rise. Holgate (2007) showed decadal rates of sea-level rise (linear trends over 10 years), but as we have shown in Rahmstorf et al. (2012), those vary wildly over time simply as a result of sampling noise and are not consistent across different data sets (see Fig. 2 of our paper). Random noise in global sea level of just 5 mm standard deviation is enough to render decadal rates meaningless (see Fig. 3 of our paper)!
The quality of the data set is important – some global compilations contain more spurious sampling noise than others. Personally I think the approach taken by Church and White (2006, 2011) probably comes closest to the true global average sea level, due to the method they used to combine the tide gauge data.
And one needs to consider boundary effects at the beginning and end of the data series. Boundary effects at the start of the curve are not a big deal because the rate curve is rather flat before the 20th Century. And luckily, at the end this is also not a big problem since we have the satellite altimeter data starting from 1993 as an independent check on the most recent rate of sea-level rise, which confirm that it is now a bit over 3 mm/year, where also the smoothed rate curve in Fig. 3 ends. We now have almost 20 years of altimeter data that show a trend consistent with the tide gauges, but less noisy, since the satellite data have good global coverage.
Conclusion
So remember: don’t fit a quadratic to data that do not resemble a quadratic. Instead, look at the time evolution of the rate of sea level rise. And remember there is something called physics: this time evolution must be expected to have something to do with global temperature. And indeed it does.
A note for the technically minded:
The quadratic fit to the sea-level curve can be written as:
SL(t) = a t^2 + b t + c, where t= time and a, b and c are constants.
The rate of rise is the time derivative:
rate(t) = 2a t + b.
Often 2a is called the acceleration. That is because when we are talking about acceleration, it is the rate of rise that is of prime interest. The question is: how does this rate of sea-level rise change over time? And not: how quadratic does the sea-level curve look? Hence the second, rate equation is the relevant one, and we call 2a and not a the acceleration in the quadratic case. 2a is the slope of the rate(t) curve.
Now the interesting thing is that in the example given above, you get a negative a when you fit a quadratic to the sea-level data in Fig. 2, but you get a positive a when you make a linear fit to the rate curve in Fig. 1. You’d probably find the latter more informative since it has to do with how the rate of rise has changed, which is the question of prime interest. But as argued above, for such a time evolution it is neither a good idea to fit sea level with a quadratic nor to fit the rate curve with a straight line – it’s a bad model that gives inconsistent results.
Matlab code:
% script to produce idealised sea level curves
x=[-50:50];
a = 1.42e-5; b = -0.0159; c=2;
rate= a* x.^3 + b*x + c;
plot([0:100],rate,’r’);
slr = cumsum(rate); % integrate the rate to get sea level
plot([0:100],slr/10,’r’);
% compute quadratic fit
p = polyfit(x,slr,2);
acceleration = 2 * p(1)
References
Church, J. A., and N. J. White (2006), A 20th century acceleration in global sea-level rise, Geophys. Res. Let., 33(1), L01602.
Church, J. A., and N. J. White (2011), Sea level rise from the late 19th to the early 21st Century, Surveys in Geophys., 32, 585-602.
Holgate, S. (2007), On the decadal rates of sea level change during the twentieth century, Geophys. Res. Let., 34, L01602.
Houston, J., and R. Dean (2011), Sea-level acceleration based on US tide gauges and extensions of previous global-gauge analysis, J. Coast. Res., 27(3), 409-417.
Rahmstorf, S. (2007), A semi-empirical approach to projecting future sea-level rise, Science, 315(5810), 368-370.
Rahmstorf, S., and M. Vermeer (2011), Discussion of: Houston, J.R. and Dean, R.G., 2011. Sea-Level Acceleration Based on U.S. Tide Gauges and Extensions of Previous Global-Gauge Analyses., J. Coast. Res., 27, 784–787.
Rahmstorf, S., M. Perrette, and M. Vermeer (2012), Testing the Robustness of Semi-Empirical Sea Level Projections, Clim. Dyn., 39(3-4), 861-875.
Wahl, T., J. Jensen, T. Frank, and I. Haigh (2011), Improved estimates of mean sea level changes in the German Bight over the last 166 years, Ocean Dyn., 61, 701-715.
“The reputable climate-statistics blogger Tamino, who is a professional statistician in real life and has published a couple of posts on this topic, puts it bluntly:
Fitting a quadratic to test for change in the rate of sea-level rise is a fool’s errand.”
And yet the same reputable Tamino seems to be engaged in a similar ‘fool’s errand’ in trying to predict future Arctic Sea Ice Extent in his recent post:
http://tamino.wordpress.com/2012/11/26/ice-free/
As some comments point out, the it is the total volume curve you need to watch here. And of course the curve could turn out sigmoidal (and likely will to some extent, considering that there will surely be some ice in the Arctic Ocean, from calving glaciers at least, during the summer for a good long time).
Some time ago, when I commented on the inappropriateness of using linear fit (“trend”) to the average temperatures I got quite a few responses regarding my post, the nicest accusing me only of silliness. Here the situation seem reversed: and I agree, for the figures presented in the post fitting a linear rate of rise seems to be obviously wrong. The smoothed line changes considerable in the presented time range. Thus I fully agree that “for such a time evolution it is neither a good idea to fit sea level with a quadratic nor to fit the rate curve with a straight line – it’s a bad model that gives inconsistent results.”
Which leaves two issues.
The first is: are the smooth lines shown in the figures a good representation of the observations? Indeed, as you write, they are not – derivatives of a noisy signal (especially when the noise is rapidly changing) are even more noisy that the sea-level basic signal. The least one would do is to draw, in the figure 3, the error-bands. Looking at figures 1 and 2 of Rahmstorf 2012, these bands would be VERY wide. Figure 6 of Houston 2011 indeed indicates such error bands (but even more importantly, it shows high frequency noise which is almost an order of magnitude larger).
The second set of questions is: what drives the sea rise? Can we go beyond the “semi-empirical” explanations? Actually, what does “semi-empirical” mean? That it is only partially based on observations? That we do not understand what is happening? If one plots the rate of change WITHOUT smoothing (or with a different smoothing parameters) does it still look similar to the temperature anomaly? Why would the DERIVATIVE of the sea level be similar to the temperature anomaly when (at least according to the IPCC report, the sea level rise is largely due to the thermal expansion of the oceans (1.6+-0.5 mm/yr). And the thermal expansion the sea level (not its derivative) depends on the temperature.
So, could you:
1. present the equivalent of figure 3 with error bands (including noise from short term phenomena)
2. present the basic physical observation (the sea level, not its derivative), again with the errors.
3. Then we could judge is a quadratic, linear or any other fitting makes sense.
Otherwise, we are again talking about data manipulation, not analysis.
[Response:
1. Our 2012 Climate Dynamics paper has this.
2. Our 2012 Climate Dynamics paper has this.
3. I recommend you have a look at it.
The interpretation of the error is not trivial though, our paper discusses this quite a bit. I believe that most of the short-term variability in the tide gauge data is due to sampling error – not anything you would be interested in linking to global temperature, so it is better to filter it out. Even if it were real physical variability, at that short time scale I would not expect it to be linked to global temperature in the way that I expect this link on longer time scales. The short-term variability of my account balance also has completely different reasons (e.g. purchase of a new stereo or a tax rebate) than the longer-term evolution (ruled by small but persistent changes in regular items like salary, housing cost …) so when you’re looking for a linkage, you must first assess on what time scale you need to be looking.
Re semi-empirical: the term reflects that this is part physics, part empirical. The physics part is that to first order, you expect the rate of continental ice melt to increase with temperature, and also the rate at which heat penetrates into the ocean below the mixed layer (for the mixed layer indeed we use a term relating temperature to sea level, not its rate of rise). The empirical part is that the equations contain parameters that need to be calibrated with observational data.
This is all in much more detail in the published papers – this is just a blog post trying to make a fairly simple point.
Stefan ]
Why a continuous curve at all? Glaciers calve suddenly. Ice sheets do the same, just much bigger. What we are seeing now is a little incidental melt and ice bits falling off the edges. When the ice sheets start progressive structural collapses we will see sea level rise events.
Take a standard structural stability analysis program as used by mining engineers, set it up for ice, and add tens of thousands of moulins. Ultimately, the ice collapses under its own weight, resulting in a high speed horizontal flow of an ice/water slurry. When this occurs in ice sheets containing half a million (or more) cubic kilometers of ice; then, there is a sea level rise event. Nobody has seen such events for a while, and all the people who saw this the last time it happened, died without recording an account.
The ice dam scenario of the Lake Missoula floods is a geologists’ fantasy. Ice dams cannot dam a liquid water head of more than about 20 feet. The water bores through the ice dam in the same process that allows moulins to form on the GIS. The Lake Missoula floods were the result of the progressive structural collapse of a canyon full of ice with super glacial ponds on top of it to form the wave benches. When the superglacial ponds got to be 6 meters deep, they drained through the ice below and triggered a progressive structural collapse. It is left to the diligent student to work out the physics of Glacial Lake Agassiz outflows. Let us just say, that a great many geologists seem not to have taken Physics X as taught by Feynman.
The entire Topex period seems to show no increase in the rate of sea level rise (about twenty years). Yet this is a period of increasing temperatures. In fact if I add the last ten years to your graph above it would have gone horizontal at the point it reached 3 mm/yr. Of course this depends on smoothing and end points, but twenty years of non increase in the rate seems significant and below the rate forecast in your papers. After all your papers on this topic were published starting in 2007 so the first 15 years of the non increasing period had already happened.
http://sealevel.colorado.edu/
[Response: The satellite altimeter data point is shown in our Vermeer&Rahmstorf 2009 paper as an independent validation point that was not used for calibration, and it fits the relationship perfectly. Remember that we are looking at a relationship on long time scales, i.e. ~15 years is one independent data point for us. If the next 15 years of altimeter data again show the same rate of rise as the last 15 years, despite further global warming, then this new data point would not fit our proposed relationship and would raise some doubts about it, but the altimeter record thus far doesn’t. -Stefan]
” if you fit a quadratic (by the standard least-squares method) to this sea-level curve, the quadratic term (i.e. the acceleration) is negative! ”
It would be nice if you stated the examples explicitly.
Wow, this is a great post. I didn’t want to bother anyone here when a denialist kept harping on “there’s no evidence of SLR acceleration,” citing http://www.sealevel.info/papers.html — into which I didn’t even investigate bec my original point was that there had been some 8″ SLR over the past 100 years, which was a factor in making the effects of Sandy worse (among other CC impacted effects), citing http://www.motherjones.com/kevin-drum/2012/11/climate-change-didnt-cause-hurricane-sandy-it-sure-made-it-worse . I had made no mention at all of SLR acceleration.
He kept harping on no acceleration and I finally told him it was a red herring and strawman to use “no SLR acceleration” to disprove CC or claim that CC could not have had any impact on Sandy, and that as far as I could see thru eyeballing the very jagged SL line over the past 100 years & extremely smoothing it in my mind’s eye I couldn’t make out overall acceleration, that I really didn’t know about acceleration only net rise, and I was not in dispute with him on his lack-of-acceleration point, but told him that lack of SLR acceleration to date (if it were so) would in no way disprove CC or whether CC had some impact on Sandy.
So that’s the new denialist tactic — there hasn’t been any drought in Texas over the past three years, ergo there’s no CC.
Fake-non-post-hoc, ergo non propter hoc.
Aaron: Are you suggesting that Glacial Lake Missoula was mostly solid ice with super glacial ponds on top of it? This is at odds with the geologic evidence. http://en.wikipedia.org/wiki/Lake_Missoula and the various references and external links.
As a physicist (but not in climate science) I can’t tell you how many times I have had to explain to students that the errors reported by their statistical fitting software are not to be trusted if they are not fitting the right function. We do not fit time series, but often are fitting with an approximate model or fitting data that has unknown experimental systematic. It is the rare case when we know the exact correct fitting function. In the case of climate time series data there is of course no “correct function”! Those MatLab packages make our lives easy, but also make it easy to get misled.
In reply to inline comments by Stefan to my post #2.
Indeed I have looked at the original papers. The problem is that the “blogosphere” simplification – namely presenting one smoothed curve (together with possibly related possibly just correlated other smoother curve) is – for me – rather cheap propagandism.
I focused on Fig 2 of Rahmstorf 2012, which shows the rate of sea level change in the form of 10 yr decadal trends. The variations reach +- 3 to 4 mm/yr. If I were to superimpose such a wide band of observational error on the Fig 3 of the blog post then – to paraphrase John von Neumann – I could fit an elephant and wiggle its trunk.
The aim of my post is: with poor resolution data (temporal noise due to multi-year oscillations, geographical noise from local ocean level increases/decreases etc.) any claim of a clear signal is dubious.
As for filtering the data, I do not believe in simple addition/subtraction. Even less in running averages: by averaging over a multiyear periods we may miss some real oscillatory phenomena that, in turn, influence the general trends. (In your “income” analogy: think of seasonal workers who earn only in certain part of the year – say beach lifeguards – and the correlation of their income with summer weather, but not with winter weather. If you average to get rid of short term variability you may very well lose the insight into the origin of the changes. I know it is a lame example – but the analogies are lame by definition… Still it may point to a real phenomenon: every simplification of data that loses the information content may lead us astray.)
Regarding your last point (and my first): while some people do read the papers (it was easy enough to google-scholar them), but others rely on blogs, especially influential ones, like this one. Thus oversimplification might create false impressions. Is it really a problem to show the error bands in the blog figure?
[Response:The point of our Fig. 2 was that 10-year linear trends are all over the place, not consistent between different data sets and mostly meaningless. You need longer-term averaging in order to be looking at the true global sea-level signal, rather than sampling noise. Note that this sampling noise in the tide gauge data most likely comes from the water sloshing around in the ocean under the influence of winds etc., which looks like sea-level change if you only have a very limited number of measurement points, although this process cannot actually change the true global-mean sea level. The longer you average, the closer you get to the true global sea level trends. Computing and interpreting what the actual uncertainty is for a given amount of smoothing is anything but trivial and ultimately remains a rough estimate. In our paper published last night in ERL we show the newer Church&White data set with less smoothing in Fig. 3 (orange line), and you can see it is more “wiggly” – hard to tell whether these wiggles are true oscillations in global sea level or again an effect of the limited number of gauges. The overall pattern remains, though: about 1 mm/year in the beginning of the century, around 1.5 – 2 mm/year in the middle of the century, rising to 3 mm/yr at the end of the century. I would link the latter, long-term evolution to global warming but not any shorter-term wiggles. -Stefan
>Ice dams cannot dam a liquid water head of more than about 20 feet
Observations of ways that ice dams form and break: http://en.wikipedia.org/wiki/Glacial_lake_outburst_flood
“Science is organized common sense where many a beautiful theory was killed by an ugly fact.” — Thomas Henry Huxley
@Wili — try reading Tamino’s article. He looks at volume, as well as extent. His article is full of weasel words and makes it clear this is not a “prediction.” However, it seems clear from observations that something big is happening, and it is happening relatively quickly. I think that is the main point of that article.
PS — arrrgh captcha!
Response to 1 – wili: If you read Tamino’s blog post… He is trying it out for fun, and to get some feel for the timescales involved. The limitations are noted. The results merit further work. ‘Nuff said?
Comment #1 by “wili” is — well, there’s no polite word for what it really is.
First of all, in the post he refers to there aren’t any quadratic fits. And, the post looked at possibilities for future sea ice area and volume, but not for extent.
I have often used quadratic fits of annual minimum Arctic sea ice extent to forecast the future value. Note the use of singular. That’s because I have warned, often and strongly, that such fits cannot be considered physically meaningful. So, I have used them to predict sea ice minimum one year into the future. As it turns out, my forecasts have been pretty successful.
I have tried to impress readers with the need for careful consideration of results rather than the insultingly simplistic approach which feeds the fake “skeptic” monster.
The post referred to extrapolates the linear trend, as estimated by a lowess smooth, to generate “what if” scenarios for the not-too-distant (but not too near) future. I emphasized, again strongly, that this was an exploratory exercise and the results shouldn’t be interpreted as “predictions.” In fact I made that explicit.
As for using volume vs area or extent, illustrating the difference in using their trends was one of the points of the post. Read it.
Now to the important point.
“Don’t estimate acceleration by fitting a quadratic” is not a law of physics. In fact, there are some situations in which it’s a useful and valid thing to do. Century-timescale sea level change is not one of them.
But one of the most common mistakes of fake “skeptics” about global warming is to apply the wrong analysis technique, which of course gives the wrong result, which they then tout as evidence against man-made global warming. The paper by Houston and Dean is one of the clearest examples of this. Usually, when such things are done it’s an honest mistake. But when fake “skeptics” do it, it’s more often just because they’re taking a simpleton’s approach to analysis. If you study the data in detail, and have the “skillz” to do so, it’s obvious that for estimating sea level acceleration on century time scales quadratic fits just ain’t right. But the fake “skeptics” don’t have the skillz. Nor do they have the will to get it right. Any tinge of subtlety or complexity confounds them. They do have the desire to get an ideologically motivated result. And that’s what they get. What a surprise.
Time series analysis isn’t just a science. It’s an art. Experience helps. You can’t just plug in some formula — quadratic or otherwise — and rely on the results, without careful consideration and study, especially when you fundamentally don’t know what you’re doing. Long practice doing it, and having learned by experience from past mistakes, also helps a helluva lot.
The simpleton’s approach to global warming science is a great way to get the wrong result. It’s also a great way to persuade the ignorant. That’s why fake “skeptics” do it so often. Thank you Stefan for such a clear illustration of why, in the case of sea level data, it’s just plain stupid.
Thank you for your response on the 2009 paper. The real question is if you had used this technique in 1997 what would have been your projection for the next fifteen years. I’m guessing that the actual rate for the period would have been significantly below what your forecast. It is easy to be in line with measurement when the model already knows the measurement. (It is often easy to be in line when you know the measurement when building the model.) When I did this analysis on the first half of the data for your 2007 paper it showed that it would have made a huge over forecast of the rate of sea level rise over the second half of the data. Of course sea level rise was fairly small during that period relative to your forecast for this century so the total difference wasn’t large.
[Response: We have a forthcoming paper where we tried your suggested experiment in a much more radical way: we forecast sea-level rise over the entire 20th Century, calibrating the model only with data from before 1900 AD. I can’t give away the results yet… -Stefan]
Gentleman, Really appreciate this forum.
A note based upon observations… we live in a punctuated equilibrium system.
When thing go, they really go!
Be it Lake Agassiz or the output of the Mississippi River system that carved a ~1 to 3km deep canyon off the Louisiana coastline and filled it halfway over the course a few instantaneous “meltwater events”.
Thanks, Stefan, for this very interesting post. I especially like that you provided us with the MATLAB code, as it made it very easy for me to reproduce and play around with your result. E.g., I tried seeing how much difference it made if one integrated the rate analytically and plotted that instead of using cumsum as a numerical approximation of the integral (answer: very little difference)…and I tried plotting the fitted quadratic too so that I could see what it looked like.
It is indeed quite counter-intuitive to me that the best-fit quadratic to the synthetic sea level curve has negative curvature even though a linear fit to the derivative of that sea level curve is clearly positive. As tamino points out, there are lots of ways that people like Houston and Dean who want to fool themselves can do so when their goal is to get a particular result rather than do a correct analysis and thus they don’t do any sort of sanity-checks on their results.
Re: Aaron Lewis @ #3:
“Take a standard structural stability analysis program as used by mining engineers, set it up for ice, and add tens of thousands of moulins. Ultimately, the ice collapses under its own weight, resulting in a high speed horizontal flow of an ice/water slurry.”
Ah, if only life and glaciers were that simple! There is a wonderful photo in Post and LaChapelle’s “Glacier Ice” that should give pause to anyone who studies glaciers and posits simple, mechanical solutions to their behavior. The photo can be seen here:
http://www.slocanlake.net/congruent_glaciers.html
For anyone who studies glaciers or loves beautiful black-and-white photography or both, “Glacier Ice, Revised Edition” is still available.
It doesn’t matter what the data looks like. Any attempt at interpolating from physical data is a fool’s errand unless you have at least a rudimentary model of the physics driving the data. Much of the denial logic relies on ignoring the physics or pretending it doesn’t count if it violates your ideology.
Both Rahmstorf (2007)and Vermeer and Rahmstorf {2009) show big uncetainties in the sea level change estimates (high standard deviations). Given that, one is only justified in concluding that the change rate is probably generally increasing, and there is really no evidence that the increase is non-linear. Modeling the trend is like modeling a blob of mayo.
Thanks, tamino and others. I stand corrected.
Stefan,
In your paper, you show that the tide gauge data falls at the low end of the uncertainty in the satellite altimeter. What is the possibility that the tide gauge data is systematically lower than the satellite data? Also, both the Wada paper and the Pokhrel paper (previously discussed at RC) show much higher SLR due to groundwater depletion. Any comments?
T. Marvell says:”Both Rahmstorf (2007)and Vermeer and Rahmstorf {2009) show big uncetainties in the sea level change estimates (high standard deviations). Given that, one is only justified in concluding that the change rate is probably generally increasing, and there is really no evidence that the increase is non-linear.”
In Figure 3, that is saying that 1 mm/yr (around 1900) is within the range 3.2 +/- 0.5 for the satellite average. Clearly erroneous.
And what to my wondering eyes should appear, but an interesting article, I found it right here!
http://iopscience.iop.org/1748-9326/7/4/044035/article (after aheads up at Climate Central..)
Curve fitting to anything other than what the underlying physics or real world mechanics supports will lead one to bad results in projections, some worse than others. You must understand your data, you cannot process it with a mathematical black box mentality. Unfortunately this requires artistic judgment in most cases, and thus the opening for curve fitter bias.
Another test is the extend the trend backwards. If you extend that curve fit backwards another 100 years, it is unlikely to make much sense against observations.
Interesting that the most accurate gauge we have, the satellite data, is not shown as a trend. This data is not noisy on an annual scale, and in fact is decelerating over the last decade from a previous nearly linear 3 mm / year since the measurements began. The tidal gauges are a mess due to regional variances and spotty coverage over a century.
I would consider the satellite data to be more reliable. This is important to some people, and not others (?). Showing the data in this way tends to make skeptical people more skeptical. It is avoiding a glaring inconsistency through graphology. Also the temperature curve not showing the recent plateau just makes one roll their eyes. Why leave oneself open to this type of criticism when it can be avoided so easily with a transparent graph of the data?
I understand this is a long term view of the data, and the satellite data is short term in this respect. However when the use of the curve fit is intended for future projections, and this fit is then used to support an argument for current and future acceleration, then not presenting the best measurement we have which does not support an argument for acceleration is misleading in my opinion.
[Response:The idea of a recent plateau in global temperature is ill-founded, see our new ERL paper, Fig. 1, where global temperature is shown as 12-months running mean. There is nothing there beyond the regular short-term variability primarily due to ENSO, and of course we should smooth enough to get rid of this short-term variability when testing for the kind of long-term linkage between global temperature and sea level that we expect. likewise your claim about the recently decelerating altimeter trend – yes if you end your analysis with the stunning recent downward spike due to La Niña. (Some people just love this short-term variability because it obscures rather than clarifies the climate evolution – it makes you not see the wood for the trees. As a climate scientist I am interested in the underlying climate evolution.) -Stefan]
[Sorry, this was meant as response to #24 but appeared separately due to some technical issue – I’ve moved it up there.]
Aaron Lewis@3: You qualify!
http://math.ucr.edu/home/baez/crackpot.html
As a geologist, I must say your stunning lack of grasp of geology is…well, kinda embarrassing.
Thanks, Tamino and Stefan et al, for this thread.
Until we have good physical models of the ice sheets, we have nothing. That is going to require much more data. Thickness, flowrates, ice temperatures, etc,
Until we have good physical models of the ice sheets, we have nothing. That is going to require much more data. Thickness, flowrates, ice temperatures, etc,
Yeah, exactly. And if you’re sitting with a block of ice in your lap and think you’re getting all wet and uncomfortable don’t worry or fidget; you’re not really wet until you’ve measured the block of ice to see if it’s getting smaller. Comfortable dryness will continue until you’ve taken enough measurements to deduce how many grams per hour of ice water are soaking into your underwear. Until you’ve got enough data just ignore that clammy sensation and don’t let your imagination run wild.
Something like that…
In a study out Tuesday, climate scientists led by Stefan Rahmstorf of Germany’s Potsdam Institute report that since 1993 sea level has risen worldwide at a rate 60% higher than predictions. from Scientists warn every inch plays a role in storms by Dan Vergano is today’s USA Today on page 3A.
I found the article entirely factual and well balanced.
1. Define “good”, and why current models aren’t good (because they’ve historically underestimated melting, therefore climatology is a fraud???)
2. Sometimes observations can be meaningful in the absence of good physical models. As an example, study the history of aviation …
#26. I find the linked paper unconvincing. Altering past projections with newly updated forcings (which are derived, not measured) and declaring the past projection as now “accurate” is uhhmmmm….cheating. I understand the argument that past projections are based on estimated future forcings which can change, but this amounts to the same things as tuning hindcasts and declaring matching a hindcast to observations as a validation of your model. Not convincing. My main response is: feel free to correctly simulate ENSO in the models. It’s hard, maybe beyond the reach of models now, but you don’t get a get out of jail free card here because you can’t simulate big drivers in the climate. If natural variability is suppressing the AGW warming, then we will see it pop back up double in the next decade or two. I’ll believe you then, but for now, color me not convinced.
[Response:It would be cheating if we had done that – but of course we have not “altered past projections with newly updated forcings” but show the past projections exactly as they were published by the IPCC in its 3rd and 4th reports. I notice you are rather quick with accusations of “misleading”, “cheating” etc. – not the style of discourse we appreciate here, even if you had gotten the basic facts right. -Stefan]
#6 Lynn, take a good look at the paper mentioned in #23, it is helpful.
Separately, since we are indirectly talking about melting ice, I recommend that people go see Chasing Ice, if you have not already. Beautiful footage of ice and glaciers, and discussion of the tragedy of the melting ice. See http://www.chasingice.com for showtimes and locations. It seems to only be playing for a week in each theater, unfortunately, so move quickly.
Thanks for the interesting post. Just as an addition if a stats package like R is used (for the above data), it will find not only the coefficients for the quadratic fit but also the standard error for the coefficient values. As the residuals of the fit are clearly correlated for this data set I am scratching my head as to whether translation of the standard errors into probabilities has a useful meaning. However, it’s clear that the x^2 term is not statistically different from zero. So really when the ‘deniers’ use this approach they are doing the same thing as always drawing conclusions from statistical noise!
I am not a denier or skeptic, but I wanted to get someone’s response to this article:
New science upsets calculations on sea level rise, climate change
Ice sheet melt massively overestimated, satellites show
http://www.theregister.co.uk/2012/11/28/sea_levels_new_science_climate_change/
[Response: There is no climate related piece of science that the Register can’t extrapolate into some shocking headline. The differences with previous data are small and technical, not ‘massively’ – unless you think they are simply using the term ‘massive’ to refer to anything with mass (which ice obviously does). The original paper is here, and for contrast you might want to read this new paper in Science too. – gavin]
Stefan,
The problem I had with the original paper, as well as the 2012 paper, is the partial disconnect of the model structure from the physical processes responsible for sea level rise. Thermal expansion and ice melt contribution would seem to be independent processes, at least to the extent that these processes evolve differently over time in response to temperature changes. The idea that the rate of ice melt contribution can be represented as a linear function of temperature increase over a “non-melting temperature” is physically reasonable, but it is hard to see how that is a reasonable model of thermal expansion. The inclusion of a negative b value for the first derivative term in the model defies physical rational… more rapid warming is expected to correspond to a faster not slower rate of rise. I think that accounting for thermal expansion separately from ice melt contribution would almost certainly be a better (and more physically reasonable) approach. Once thermal expansion is subtracted from the tide gauge record, the remaining rise should better fit the ice melt model, and give an improved overall fit, without the need for a derivative term.
[Response: We applied the Vermeer&Rahmstorf model separately to thermal expansion, and it works really well. This is because (a) the rate of heat penetration into the deeper ocean increases in proportion to temperature (like for ice melt), and (b) the second term we added models the mixed layer response successfully. (And when applied to thermal expansion, b is positive and the number is consistent with typical mixed layer depths in the ocean.) So I think the equation does correspond to the relevant physical processes. Why b is then negative for the fit to the overall observed sea-level rise remains a bit of an enigma, though – in our paper we interpret this as a time lag, and I still think this is the likely answer. It warrants further investigation, though. -Stefan]
Estimate of polar land-ice melt – .6 mm/yr increase in sea level:
http://www.sciencemag.org/content/338/6111/1183.abstract
http://www.npr.org/2012/11/23/165667600/an-arbor-embolism-why-trees-die-in-drought
corrected NPR link
http://www.npr.org/2012/11/29/166176294/iceismeltingfaster
Do the RC team plan to comment on the new science paper ( linked by Gavin in the comments) on ice sheet melting? I’d be interested to see your views.
I just finished reading the paper by Shepherd et al. in tomorrow’s Science
that Dr. Schmidt pointed out, and I reproduce some numbers from Table 1
GRIS 1993-2003 -83 +/- 63
GRIS 2005-2010 -263 +/- 30
APIS 1993-2003 -12 +/- 17
APIS 2005-2010 -36 +/- 10
WAIS 1993-2003 -49 +/- 31
WAIS 2005-2010 -102 +/- 18
These are the numbers in Gt/yr for rate of mass waste for the indicated regions and time periods. GRIS quadrupled, APIS tripled, WAIS doubled in a decade.
That’s quite some acceleration…
sidd
I have posted a copy of Fig 5 from the Shepherd et al. paper at
http://membrane.com/sidd/Shepherd-2012-fig5.png
APIS,GRIS mass waste rates are supralinear (oh, no!), WAIS seems linear (oh, better!) except lately (oh, no! again…)
sidd
The following may sound to many trivial, but may make some things clearer for others.
Concerning the topic of the “correct fitting function” and the errors of it: any assumption of a function fitting to a set of data is an implicit assumption of a class of physical models, and its value lies not in itself but in its predictive capability. Of two such functions/model classes with seemingly equal fitting capability for the past, any of them or both may be of bad predictive capability. So to find a fitting function worthy of some trust one has to make the implicit model explicit – as an approximative expression of real physical processes.
GCMs are such explicit approximations, so they are the candicates of choice to produce a fitting curve. Their adavantage is also their disadvantage: their complexity makes an understanding of the big picture by us humans nearly impossible. So we have to resort to some medium to low complexity model. Of the sort: thermal expansion rate ~ heat flow rate into the ocean ~ temperature anomaly. With net melting rate, things are much more complex, because the snowfall/melting balance is involved, but at least some approximative model of low complexity can also be worked out.
Returning the original post, this is helpful to point out and, most fundamentally, it calls all authors to publish the model they are actually fitting (and reviewers to require them to do so) and be clear how what is reported in text relates to the model.
That is, are authors reporting on sea level or ice sheet acceleration reporting a or 2a? In all cases I looked at recently there was no statement of what was actually being reported beyond stating that the authors were fitting a “quadratic” or “acceleration” term.
Gavin, inline response to #34:
Yeah, I used to really enjoy El Reg, until it became clear there was an editorial policy of AGW denial at the site. I wish I knew the story of how that came to be.
I find Houston & Dean 2011 is so flawed that you could write a book correcting all its misdemeanours.
There is however something profound missing both from it & from that criticising it. Nobody has properly presented the SLR data graphically (although a few well-smoothed thumbnails are provided/linked here) which would show what the fuss is all about. H&D2011 attempts to summarise future SLR as a single average ‘acceleration’ but the only graph of SLR they provide (as their fig 5) is is not theirs at all but one from Holgate 2007.
Given these two geriatrics Houston & Dean are incapable of it, I had a go myself on the Church & White data they say shows a negative ‘acceleration’ and produced this graph.
Their choice of 1930 as a start point is not entirely unreasonable in itself, a way of disentangling the obvious ‘acceleration’ that occurred in the earlier parts of the 1900s. Their end points were probably chosen for them by the available Church & White data but these are evidently unfortunate choices for end points. The present 2009 end to the Church & White data is likely also a poor choice, probably overstating the 1930-2009 linear regression (just as ending in 2001 & 2007 understated it).
My graph does beg the question “Why the ‘potholes’ in both the 60s & 80s?” Beyond that, I’d take away a rough SLR ‘acceleration’ for 1930-2009 of something like 0.15mm/yr/yr by ignoring these ‘potholes.’ There is certainly evidence for an ‘acceleration’ that H&D2011 deny exists. Then, these are the same two gentlemen who give ‘acceleration’ to 4 decimal places when one of their references Douglas 1992 (fig 3) shows an expected scatter from such data as +/- 1mm/yr/yr.