It is a good tradition in science to gain insights and build intuition with the help of thought-experiments. Let’s perform a couple of thought-experiments that shed light on some basic properties of the statistics of record-breaking events, like unprecedented heat waves. I promise it won’t be complicated, but I can’t promise you won’t be surprised.
Assume there is a climate change over time that is U-shaped, like the blue temperature curve shown in Fig. 1. Perhaps a solar cycle might have driven that initial cooling and then warming again – or we might just be looking at part of a seasonal cycle around winter. (In fact what is shown is the lower half of a sinusoidal cycle.) For comparison, the red curve shows a stationary climate. The linear trend in both cases is the same: zero.
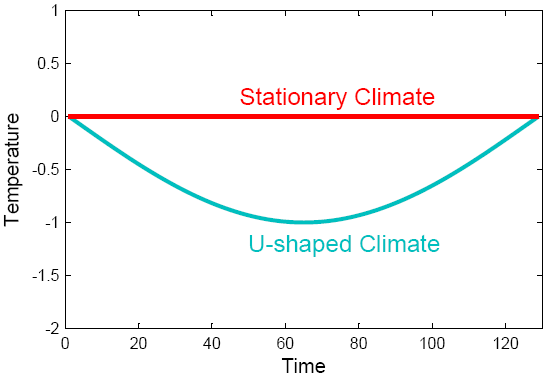
Fig. 1.Two idealized climate evolutions.
These climates are both very boring and look nothing like real data, because they lack variability. So let’s add some random noise – stuff that is ubiquitous in the climate system and usually called ‘weather’. Our U-shaped climate then looks like the curve below.
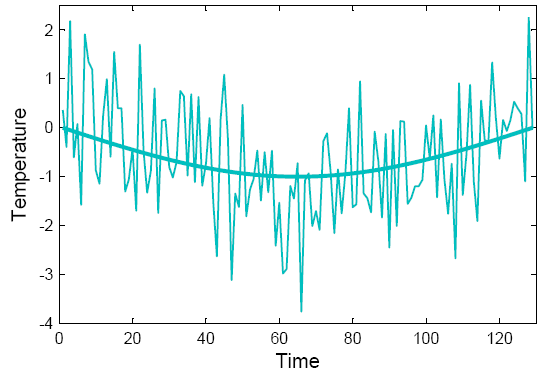
Fig. 2. “Climate is what you expect, weather is what you get.” One realisation of the U-shaped climate with added white noise.
So here comes the question: how many heat records (those are simply data points warmer than any previous data point) do we expect on average in this climate at each point in time? As compared to how many do we expect in the stationary climate? Don’t look at the solution below – first try to guess what the answer might look like, shown as the ratio of records in the changing vs. the stationary climate.
When I say “expected on average” this is like asking how many sixes one expects on average when rolling a dice a thousand times. An easy way to answer this is to just try it out, and that is what the simple computer code appended below does: it takes the climate curve, adds random noise, and then counts the number of records. It repeats that a hundred thousand times (which just takes a few seconds on my old laptop) to get a reliable average.
For the stationary climate, you don’t even have to try it out. If your series is n points long, then the probability that the last point is the hottest (and thus a record) is simply 1/n. (Because in a stationary climate each of those n points must have the same chance of being the hottest.) So the expected number of records declines as 1/n along the time series.
Ready to look at the result? See next graph. The expected record ratio starts off at 1, i.e., initially the number of records is the same in both the U-shaped and the stationary climate. Subsequently, the number of heat records in the U-climate drops down to about a third of what it would be in a stationary climate, which is understandable because there is initial cooling. But near the bottom of the U the number of records starts to increase again as climate starts to warm up, and at the end it is more than three times higher than in a stationary climate.
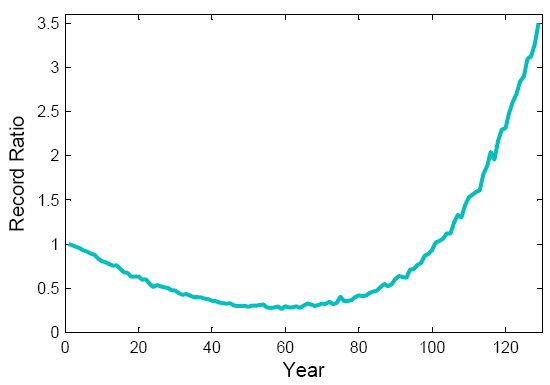
Fig. 3. The ratio of records for the U-shaped climate to that in a stationary climate, as it changes over time. The U-shaped climate has fewer records than a stationary climate in the middle, but more near the end.
So here is one interesting result: even though the linear trend is zero, the U-shaped climate change has greatly increased the number of records near the end of the period! Zero linear trend does not mean there is no climate change. About two thirds of the records in the final decade are due to this climate change, only one third would also have occurred in a stationary climate. (The numbers of course depend on the amplitude of the U as compared to the amplitude of the noise – in this example we use a sine curve with amplitude 1 and noise with standard deviation 1.)
A second thought-experiment
Next, pretend you are one of those alarmist politicized scientists who allegedly abound in climate science (surely one day I’ll meet one). You think of a cunning trick: how about hyping up the number of records by ignoring the first, cooling half of the data? Only use the second half of the data in the analysis, this will get you a strong linear warming trend instead of zero trend!
Here is the result shown in green:
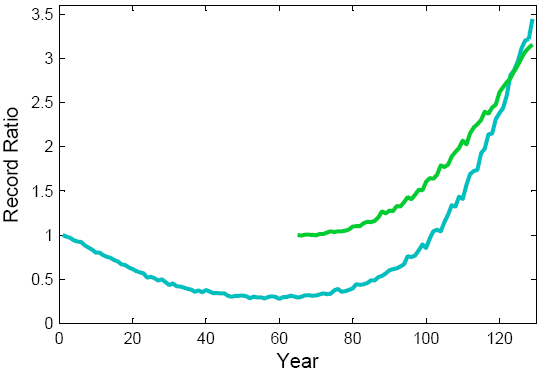
Fig. 4. The record ratio for the U-shaped climate (blue) as compared to that for a climate with an accelerating warming trend, i.e. just the second half of the U (green).
Oops. You didn’t think this through properly. The record ratio – and thus the percentage of records due to the climatic change – near the end is almost the same as for the full U!
The explanation is quite simple. Given the symmetry of the U-curve, the expected number of records near the end has doubled. (The last point has to beat only half as many previous points in order to be a record, and in the full U each climatic temperature value occurs twice.) But for the same reason, the expected number of records in a stationary climate has also doubled. So the ratio has remained the same.
If you try to go to even steeper linear warming trends, by confining the analysis to ever shorter sections of data near the end, the record ratio just drops, because the effect of the shorter series (which makes records less ‘special’ – a 20-year heat record simply is not as unusual as a 100-year heat record) overwhelms the effect of the steeper warming trend. (That is why using the full data period rather than just 100 years gives a stronger conclusion about the Moscow heat record despite a lesser linear warming trend, as we found in our PNAS paper.)
So now we have seen examples of the same trend (zero) leading to very different record ratios; we have seen examples of very different trends (zero and non-zero) leading to the same record ratio, and we have even seen examples of the record ratio going down for steeper trends. That should make it clear that in a situation of non-linear climate change, the linear trend value is not very relevant for the statistics of records, and one needs to look at the full time evolution.
Back to Moscow in July
That insight brings us back to a more real-world example. In our recent PNAS paper we looked at global annual-mean temperature series and at the July temperatures in Moscow. In both cases we find the data are not well described by a linear trend over the past 130 years, and we fitted smoothed curves to describe the gradual climate changes over time. In fact both climate evolutions show some qualitative similarities, i.e. a warming up to ~1940, a slight subsequent cooling up to ~ 1980 followed by a warming trend until the present. For Moscow the amplitude of this pattern is just larger, as one might expect (based on physical considerations and climate models) for a northern-hemisphere continental location.
NOAA has in a recent analysis of linear trends confirmed this non-linear nature of the climatic change in the Moscow data: for different time periods, their graph shows intervals of significant warming trends as well as cooling trends. There can thus be no doubt that the Moscow data do not show a simple linear warming trend since 1880, but a more complex time evolution. Our analysis based on the non-linear trend line strongly suggests that the key feature that has increased the expected number of recent records to about five times the stationary value is in fact the warming which occurred after 1980 (see Fig. 4 of our paper, which shows the absolute number of expected records over time). Up until then, the expected number of records is similar to that of a stationary climate, except for an earlier temporary peak due to the warming up to ~1940.
This fact is fortunate, since there are question marks about the data homogeneity of these time series. Apart from the urban adjustment problems discussed in our previous post, there is the possibility for a large warm bias during warm sunny summers in the earlier part, because thermometers were then not shaded from reflected sunlight – a problem that has been well-documented for pre-1950 instruments in France (Etien et al., Climatic Change 2009). Such data issues don’t play a major role for our record statistics if that is determined mostly by the post-1980 warming. This post-1980 warming is well-documented by satellite data (shown in Fig. 5 of our paper).
It ain’t attribution
Our statistical approach nevertheless is not in itself an attribution study. This term usually applies to attempts to attribute some event to a physical cause (e.g., greenhouse gases or solar variability). As Martin Vermeer rightly said in a comment to our previous post, such attribution is impossible by only analysing temperature data. We only do time series analysis: we merely split the data series into a ‘trend process’ (a systematic smooth climate change) and a random ‘noise process’ as described in time-series text books (e.g. Mudelsee 2010), and then analyse what portion of record events is related to either of these. This method does not say anything about the physical cause of the trend process – e.g., whether the post-1980 Moscow warming is due to solar cycles, an urban heat island or greenhouse gases. Other evidence – beyond our simple time-series analysis – has to be consulted to resolve such questions. Given that it coincides with the bulk of global warming (three quarters of which occurred from 1980 onwards) and is also predicted by models in response to rising greenhouse gases, this post-1980 warming in Russia is, in our view, very unlikely just due to natural variability.
A simple code
You don’t need a 1,000-page computer model code to find out some pretty interesting things about extreme events. The few lines of matlab code below are enough to perform the Monte Carlo simulations leading to our main conclusion regarding the Moscow heat wave – plus allowing you to play with the idealised U-shaped climate discussed above. The code takes a climate curve of 129 data points – either half a sinusoidal curve or the smoothed July temperature in Moscow 1881-2009 as used in our paper – and adds random white noise. It then counts the number of records in the last ten points of the series (i.e. in the last decade of the Moscow data). It does that 100,000 times to get the average number of records (i.e the expected number). For the Moscow series, this code reproduces the calculations of our recent PNAS paper. In a hundred tries we find on average 41 heat records in the final decade, while in a stationary climate it would just be 8. Thus, the observed gradual climatic change has increased the expected number of records about 5-fold. This is just like using a loaded dice that rolls five times as many sixes as an unbiased dice. If you roll one six, there is then an 80% chance that it occurred because the dice is loaded, while there is a 20% chance that this six would have occurred anyway.
To run this code for the Moscow case, first download the file moscow_smooth.dat here.
----------------------
load moscow_smooth.dat
sernumber = 100000;
trendline = (moscow_smooth(:,2))/1.55; % trendline normalised by std dev of variability
%trendline = -sin([0:128]'/128*pi); % an alternative, U-shaped trendline with zero trend
excount=0; % initialise extreme counter
for i=1:sernumber % loop through individual realisations of Monte Carlo series
t = trendline + randn(129,1); % make a Monte Carlo series of trendline + noise
tmax=-99;
for j = 1:129
if t(j) > tmax; tmax=t(j); if j >= 120; excount=excount+1; end; end % count records
end
end
expected_records = excount/sernumber % expected number of records in last decade
probability_due_to_trend = 100*(expected_records-0.079)/expected_records
----------------------
Reference
Mudelsee M (2010) Climate Time Series Analysis. Springer, 474 pp.
I am currently (re)reading two books by William Feller:
An Introduction to Probability Theory and its Applications,
Volumes 1 (3rd edition, 1968) & 2 (2nd edition, 1971),
John Wiley & Sons, Inc.
which are particularly strong on random walks.
Regarding Moscow (Moscow Oblast) and more widely Eastern Europe/Central Asia temperature excursion of 2010, first note that records are considered to be adequate to determine this was a unprecented event in recorded history (ca. 1000 years). Now treat the temperature changes from one August to the next as a random walk starting from the average temperature. Assuming no trend, we have from Feller 1:III(7.3) that … roughly speaking, the waiting time for the first passage through r [positive increments] increases with the square of r; the probability of a first passage after epoch (9/4)r^2 has a probability close to (1/2).
If a trend is included, consider the Fokker-Plank diffusion equation of 1:XIV(6.12) which diffuses probabilities for random walks with an advection term. While this directs us to 2:X for the continuous case, we can see enough here to replace r by r-ct due to the advective drift.
While there is an important lesson here, I suppose one might care to check whether treating the temperatures as a random walk (with or without drift) otherwise seems to accord with the (all too short) temperature record.
[The reCAPTCHA oracle entones “Statistics taitivi”.]
Dan H, Cris R.
The increase in the probability of high sigma events will be strongly affected by a change in the mean. Just look at how quickly the gaussian distribution drops off as sigma increases. So while the increase in the number of one sigma events won’t be very spectacular, the increase in (formerly) five sigma events will be overwhelming.
Thanks for this post.
Various denier blogs seem to be hailing as some sort of evidence that climate change won’t be damaging (or doesn’t exist), the impending IPCC Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. As per normal, they seem to equate uncertainty with ‘not happening’.
It would be useful to have an article here on RealClimate discussing the report and highlighting the important messages in it after it’s been released.
Richard Black has an article here that to my mind doesn’t further understanding a whole lot – not because it’s wrong but because of the slant he takes (which isn’t necessarily wrong either, but is written in a way that makes it easier for deniers to twist and run with the wrong message).
http://www.bbc.co.uk/news/science-environment-15698183
(Captcha = mischief)
Norm Hull (97) wrote:
Norm, when we talk about global warming we are referring to the global average temperature anomally as it changes over time. There is no rule that says it has to be uniform, either with respect to time or place. As dhogaza points out (99) land warms more rapidly than ocean given the ocean’s greater thermal inertia, the Northern Hemisphere warms more rapidly than the Southern Hemisphere given its greater landmass, the continental interiors warm more rapidly than the coasts given their distance from the ocean where the warming is then amplified by their falling relative humidity, the poles warm more rapidly than the equatorial regions given a variety of mechanisms collectively referred to as “polar amplification”, nights more rapidly than days given that an enhanced greenhouse effect is driving global warming rather than enhanced solar insolation, winters more rapidly than summers for the same reason, and higher latitudes more rapidly than lower latitudes.
For the last of these please see Tamino’s post:
Hit You Where You Live
Tamino, Jan 11, 2008
linked to at http://www.skepticalscience.com/open_mind_archive_index.html
… and note that Moscow is at a latitude of 55.45 N.
Norm Hull (97) wrote:
Your estimate of Joseph Romm and mine no doubt differ a great deal, but setting that aside, I wasn’t quoting Joe Romm. As I made clear(88), I was quoting Trenberth, one of the foremost experts in climatology, who was providing the very sort of physical explanation you were calling for. Not that I thought it was needed or that you would be particularly interested, and your attempt to conflate the two individuals would seem to prove me right. But for the sake of those who might be, I thought it worthwhile to provide a link.
Norm Hull:
Romm’s an MIT PhD physicist so I doubt his criticisms of Muller are simply because Muller criticized some of Al Gore’s “exaggerations”, particularly since the latter don’t really exist …
You also seem to be implying that Trenbreth’s guilty of making political, not scientific, statements … but what is your proof?
Whatever, you’re not exactly raising the banner high for objective scientific discourse yerself.
Just saying’
Thomas,
The probability of high sigma events does not change appreciably as the mean changes, precisely because they are high sigma.
[Response: No, no, NO! The probability of high sigma events changes rapidly as the mean of the distribution shifts (assuming a non-uniform distribution). Think about it.–Jim]
The event which unfoldeded in Russian has a low probability of occurrance (call it the 2.5% upper tail). However, once the event occurs, the actual temperature recorded is not part of a Gaussian distribution. The blocking was stronger than previously, and the mercury broke the record set in 1936. That is two events, 74 years apart, which fit within the upper tail. The event falls within the tail, not the recorded temperature.
Look at the temperature history. Moscow broke the record high temperature last year, which was previously set in 1936. Many U.S. cities set high temperatures in 1936 which still stand. The probability of the weather conditions occuring, as in 2010 or 1936, remains the same.
[Response: This stuff varies from wrong to irrelevant.–Jim]
“The probability of high sigma events changes rapidly as the mean of the distribution shifts (assuming a non-uniform distribution).”
Did you mean the probability of what used to be high sigma events on one side of the distribution?
[Response: Yes]
Individual regional events are always going to be difficult to relate to global climate change.
Surely the record to concentrate on is the global temperature record.
Now if the assumption is that the Earth is warming at 0.2c per decade, then if a new record is not set within 8 years of the past record, then the assumption will be disproven at the 95% level.
Looking at Hadcrut this level was passed in 2006 and there is no chance of 2011 breaking the record and I woiuld be willing to bet a very large amount that 2012 wont do so either given the current ENSO state.
If we look at the probability of the current record being broken by a significant amount of at least 0.1c then approx 18 years would have to pass to disprove the assumption at the 95% level.
None of the global databases have seen such a new record since 1998. If no new significant record is set by 2016, will scientists have to agree that the current assumption is wrong?
[Response: No, they will have to agree that your assumptions are wrong. Even if I assume your calculations are right, you’re wrongly assuming absolute linearity of T change. Also the paper did also dealt with the setting of global T records. Both of these you would have recognized had you read and understood the paper.–Jim]
Alan
For Timothy Chase on 104,
I was not saying that global warming would be uneven. I was saying you need to do some work to claim the warming in the last 30 years was all global warming, but that warming and cooling for the 100 years before that should be discounted. I don’t think looking at the clear temperature variability, that you can just claim all of moscow’s warming in the last 30 years is clobal warming. Was the cooling in moscow also caused entirely by global warming? I’m not aguing about all of it, only that someone needs to do an attribution of how much. NOAA seems to have some clear GISS data.
[Response: That’s not what the paper is claiming, or is even about really.]
As to 105 and your contention, I don’t think any of Trenbreth’s criticism actually stand up to any real scrutiny. You will note he doesn’t find anything that is disputed by science. The author of this article did bring up some points about dole that are scientific in nature, and NOAA quickly started examining them. I would prefer scientific arguments, and not to argue about whether Climate Progress or WUWT stick mainly to science. Trenbreth’s main opinion on attribution studies is if they do not find attribution they are wrong. Trenbreth believes everything in weather is attributed to man, and does not want to check the data, because if it disagrees it must be a type 2 error. He has been quite vocal about this. I would take any of his scientific problems with the study seriously, but he doesn’t seem to have any real disputes.
[Response: Nonsense. Read the paper and contribute something worthwhile or have your off the cuff nonsense deleted–Jim]
Chris G,
Sorry I missed your post. I’d like to say I’m glad to see someone else is alarmed by the Hansen paper, although given the situation that somehow doesn’t seem appropriate.
Norm Hull,
Why have you shifted the subject to Barriopedro et al????
That said the quote you post opens with “The enhanced frequency for small to moderate anomalies of 2-3 SDs is mostly accounted for by a shift in mean summer temperatures”. In view of which you might like to add this to your reading list: “Greenhouse forcing outweighs decreasing solar radiation driving rapid temperature rise over land.” Phillipona & Durr 2004. It complements the Barriopedro paper rather well.
Now back to the matter at hand: The paper by Hansen, Ruedy and Sato (Hansen’s paper). You have failed to address the points made in my post #94.
1) Do you accept that the SD is not incorrect and that Hansen’s observations are not random chance?
2) Do you accept that the increase in areas covered +2 and +3 sigma temperature excursions (figure 4) is a real increase?
Jim says:
15 Nov 2011 at 12:21 PM
[Response: No, they will have to agree that your assumptions are wrong. Even if I assume your calculations are right, you’re wrongly assuming absolute linearity of T change. Also the paper did also dealt with the setting of global T records. Both of these you would have recognized had you read and understood the paper.–Jim]
The 0.2c per decade is certainly not my assumption, as I see nothing in the temperature records of the 20th and 21st centuries which remotely suggests that the Earth is warming at this rate, unless you look at short cherry picked periods.
The probability calculations, of course, do not assume a near linear yearly increase in temperatures as I am fairly sure that if that was the case we would get a new record far more often!
The probability of new records being set is a good way of checking assumptions, as it does not require us to wait for 30 or 40 years to check these temperature assumptions.
After all to get from one place to another we have to go on a journey. I am sure noone has suggested that we are going to wake up on 1/1/2100 and find that the temperatures rose 2.0c overnight!
Assuming a linear increase in CO2, the first decades of the 21st century should have the strongest forcing effect making new recorde more likely than the last decades of the century. I know that CO2 increase seems to be increasing slightly faster than linear but this just makes it even more probable that a new record should be set, in the timescales I have given.
Science has to use probabilities in assessing assumptions.
Of course, just because an assumption has failed at the 95% level doesn’t mean it is definitely false, but that is the level most scientists have set that would require assumptions to be revisited and very strong evidence to be produced if it was not to be altered.
I don’t think many papers are being quoted out there that have failed at the 95% level.
[Response: What?–Jim]
Alan
Dan H., “The probability of high sigma events does not change appreciably as the mean changes, precisely because they are high sigma.”
Utter crap. The mean and standard deviation are uncorrelated only for the normal distribution. If the data are not normal–and far from the mean they likely are not, you simply can’t make such a claim.
Chris G.
I was not trying to shift the subject, I was trying to address one of your points. I apologize if that did not come across correctly.
In answer to your two points
1) Do you accept that the SD is not incorrect and that Hansen’s observations are not random chance?
I do not think that Hansen’s observations are random chance, but neither do I think that all of these events are properly ascribed to 3 SD independent probabilities. If events are individual and properly modeled, the probability of any single one exceeding 3SD in the positive direction is slightly more than 0.1%. If there is a great many exceeding this threshold than the model needs to be corrected. There may be something happening that causes a temporary directional shift, or increased variation, or coupling of these events. I would like to see new models especially ones of extreme drought/heat, flood/heat analyzed. Stefan Rahmstorf and Dim Coumou are testing if a different model for trend line which may alter probabilities.
2) Do you accept that the increase in areas covered +2 and +3 sigma temperature excursions (figure 4) is a real increase?
I do. This doesn’t mean I have examined the data, but I assume its correct, and the authors are good enough scientists to correct it if they have anything wrong.
Alan Millar: for entertainment purposes, can you please tell us how you calculate that “95% level” and how you assess that climate predictions have “failed” it?
Re: 106, 107, 112 (change in mean and high-sigma events)
I think that all of you arguing with Dan H. are forgetting the traditional goal-post shift that skeptics use. As soon as the mean goes up, the goal-post for “high-sigma events” goes up, so normal gets redefined and nothing unusual is happening. “Extraordinary” events just don’t happen, because when they do they get re-incorporated into the definition of normal, and now that they are part of normal, they can’t possibly be abnormal, can they?
> the first decades of the 21st century should have the strongest forcing
Got that backwards, doesn’t he?
Several commenting here recently seem to have ignored the lesson from my earlier comment.
114 toto says:
15 Nov 2011 at 3:54 PM
“Alan Millar: for entertainment purposes, can you please tell us how you calculate that “95% level” and how you assess that climate predictions have “failed” it?”
The figures come from the IPCC models themselves.
By checking the average waiting time for a new record from all the models, gives approximately 8 years for any new record and 18 years approximately for a significant new record of at least 0.1c at 95% confidence level.
Of course, if the Earth has a very high natural variability, outside that contained in the models, then you could expect to wait longer.
[Response: Are you seriously claiming *you* calculated this? The calculations were presented in our 2008 post. Please do not play games. – gavin]
However a very high natural variability would cause significant problems for the models, their accuracy, and predictive ability.
116 Hank Roberts says:
15 Nov 2011 at 5:37 PM
“the first decades of the 21st century should have the strongest forcing
Got that backwards, doesn’t he?”
CO2s effect is logarithmic in nature and it is clear therefore, with a linear increase in CO2, the forcing effect is stronger in the first decades than the last. Even a small exponential increase (eg first decade 20ppm increse, 2nd 21ppm increase, 3rd 22ppm etc) would derive a weaker forcing effect in the last decade compared to the first.
A larger exponential increase would indeed produce a stronger forcing effect as time passed.
Alan
> millar … co2 forcing
We were talking about observable effects on Earth’s climate.
You’re talking now about CO2 alone, considered separate from everything else?
Differently placed goalpost, I think.
The effects — climate change — are not going to emerge clearly from natural variability in the early decades.
Re 108 and 118,
Gavin do think anything has changed to change the probabilities in your models (95% confidence of a new record of at least 0.1 degree C above the last record temperature)? I don’t think Jim’s comment that understanding this paper would change your projections, but I wanted to make sure I wasn’t missing something.
[Response: The calculations done on the IPCC models, were simply a counting exercise – no complicated statistics used. But there are some issues that are worth bearing in mind when applying this to the real world. First, the global temperature products are not exactly the same as the global mean temperature anomaly in the models (this is particularly so for HadCRUT3 given the known bias in ignoring the Arctic). Second, both 2005 and 2010 were records in the GISTEMP and NCDC products (I think). Third, the models did not all use future estimates of the solar forcing for instance, and for those that did, they didn’t get the length and depth of the last solar minimum right. This might make some small difference (as would better estimates for the internal variability, aerosol forcing etc.). But as an order of magnitude estimate, I think the numbers are still pretty reasonable. – gavin]
119 Hank Roberts says:
15 Nov 2011 at 8:02 PM
“millar … co2 forcing
The effects — climate change — are not going to emerge clearly from natural variability in the early decades.”
Hank, I kind of agree with you.
This was the issue that first caused me to doubt the AGW meme.
I always used to accept the fact of AGW. I assumed the consensus position must be true because my experience in science did not lead me to think that significant obvious flaws could be overlooked.
However, when the prognosis for Mankinds future became quite apocolyptic I decided to look closer at the facts. That is when, almost immediately, I saw the most obvious flaw in the arguement.
The predictions for the future were largely based on climate models and it was said that we could rely on these models for the future because they were accurate on the backcast. Yes, when I looked they were quite accurate against the temperature record since 1945.
That is when my doubts arose!
They were too accurate against the temperature record!
Why?
Because they are not measuring the same thing!
The GCMs measure and output the climate signal only. The weather signal and cycles, such as ENSO, are averaged out. The temperature record is the climate signal PLUS the weather signal. We know, as you have recognised Hank, that the weather signal can swamp the climate signal over short periods even as long as a decade. The climate signal will however re-emerge in the medium to long term.
So I found that, on the backcast, the GCMs matched the decadal temperature directions but failed to do so on the forecast. Big red flag for me!
Not because they have failed to match the direction of the last decade, I would actually expect that to happen fairly often with a reasonably high natural variability, but that they matched so well on the backcast. Two things matching so well when they are not measuring the same thing?
Hmmm…..
Alan
Bob,
I think you are missing the point. Ray and Pete are not arguing that these events will become normal in a warmer world, but that they will become more prevalent. My argument was that their probability will not change, because they are well beyond the 2 sigma range. Your “goal post” shift argument does not adequately reflect our discussion here. Personally, I do not feel that Ray, Pete, or anyone else debating the occurrance of these types are events are arguing that they will become normal, and therefore, cease to become “extraordinary.”
Dan H.
That’s crud
Put 1/millionth of a point on a die and the odds of rolling 1 to 6 will change.
Dan H. @122 — Let N[m,s] denote the normal probability density with mean m and standard deviation s. Consider (positive) event e such that for N[0,s], p(e) is at the 3.5s level. What is the probability of e for N[1,s]? N[2,s]? N[3,s]?
Alan Millar
No, individual model runs show such variation, ENSO-like events, etc.
Model *ensembles* don’t, just as aggregating an ensemble of coin flips doesn’t (while records of each individual series shows variability such as 3 or 4 heads in a row).
Your skepticism is based on a misunderstanding as simple as this?
The mind boggles.
[Response: Indeed, GCMs also simulate weather, albeit at a coarser scale (though increasingly at a fine scale). And indeed, even model ensembles tend to capture ENSO quite well, since it is pretty fundamental to the physics of the system.–eric]
Alan Millar…
Besides the fact that your entire line of thinking is flawed, anyway.
Airliner design is mostly based on models that aren’t really different than GCMs. The scale is smaller (individual airplanes are smaller than the earth – I’m sure you’ll agree with this). But the events being modeled are similarly finer-grained.
No model is able to accurately plot the path of an individual molecule in the air over a wing or other surface.
It’s all done by the equivalent of model ensemble techniques.
Yet … despite your lack of faith … they fly.
Big red flag for me, too, because you first state that natural variation can swamp the climate signal, then proclaim that the fact that we’ve been seeing natural variation (in particular, in the sun’s output) dampen the climate signal (but not significantly) tells you the climate science is all hooey.
Sort of a tautology denial of some sort …
The 787 simulator built to train pilots was developed, tested, and used to train the first pilots to fly the plane BEFORE IT EVER FLEW, and on its first test flight, performed exactly as the model had taught the pilots to expect it to.
> as you have recognised Hank
Nope, you still have it backwards.
Norm Hull wrote in 85:
Norm Hull wrote in 113:
Do you make a habit of learning things in reverse?
Alan Millar,
So, you rejected the science because you didn’t understand it that over short periods, variability could mask trend? That’s brilliant. Dude, you know, somehow your conversion story isn’t quite as compelling as that of St. Augustine.
Ray,
It does not appear that Alan rejected the science, only the models. The models behaved quite well during a period of solar and ocean activity which generally contributed to higher temperature observations. It wasn’t that the GCMs couldn’t model short term variability, but that the short-term variability became part of the model.
[Response: How did observed ‘short term ocean activity’ become ‘part of the model’? – gavin]
127 Hank Roberts says:
16 Nov 2011 at 1:16 AM
“Nope, you still have it backwards”
129 Ray Ladbury says:
16 Nov 2011 at 7:54 AM
“Alan Millar,
So, you rejected the science because you didn’t understand it that over short periods, variability could mask trend? That’s brilliant. Dude, you know, somehow your conversion story isn’t quite as compelling as that of St. Augustine.”
I must be living in some sort of alterate reality here.
One. Where logarithmic effects gets stronger as time progresses. And.
Two. Where my words are translated to mean the exact opposite of their true meaning!
I said the rreason I started to doubt the models predictions was because they were too accurate on the backcast not that that they are inaccurate on a period of a decade on the forecast.
Again!! if the Earth has a fairly high natural variability I would expect the models signal to be constantly swinging between overstating and understating the warming with the true signal emerging in the medium to long term.
The models signal from 1945 did not do this to any great extent and I find that very strange, given that they are not set upto match the short term (decadal) trend of the temperature record with its inclusion of the weather signal (natural variability).
That is the reason given for the models signal not matching the past decades temperature trend. That, I don’t find strange, if the models are set up accurately.
The proof of the pudding will be if the temperature trend swings back the other way and the models climate signal emerges from the natural noise.
Alan
Re: Dan H 2 122
You said “My argument was that their probability will not change, because they are well beyond the 2 sigma range.”.
As the temperature distribution shifts due to climate change, probabilities will change at every absolute temperature. Thus, the previous probability at temperature T will no longer apply. What used to be +3 sigma in the old distribution may now only be +2 sigma (if the shift in the mean is equal to +1 sigma) in the new distribution, which has a higher probability.
The only way to keep the probability constant is to say “+ 3 sigma in the new distribution has the same probability as +3 in the old distribution”, which requires that you be talking about two different temperatures in the two different distributions. You can’t do that if you are looking at the probability of a specific temperature T, which is the goal of the study.
It would appear that you don’t even realize you are shifting goalposts.
Bob Loblaw on 132,
I think you are mistaking proper statistical modeling for some sort of conspiracy. There are two different issue’s here. If you are going to properely model the system and figure out what the 3 sigma probability is, then you need to model the distribution properly, this is not moving goal posts its proper statistical modeling. In fact this article is written to help explain a paper that was talking about how to do these statistics.
IMHO we all can agree that the Russian Heat Wave was an extreme weather event. I think this is what you mean by goal posts. Then the question is what defines an extreme weather event. There will be disagreement on this, and I don’t want to bring all this up here. Once this is defined you can use statistics, but you will not get a proper probability if you get the distribution of temperature or precipitation wrong.
Alan Millar,
When we hindcast, we know what the fricking weather was. We know what ENSO did. We know if there were volcanic eruptions. We know what the sun did. Why shouldn’t we get better hindcasts? Dude, this ain’t that tough!
Norm Hull, The Moscow heatwave was an extreme event–by definition, since it was a record. If changes in the standard deviation were dominant, we’d expect to see a symmetry between record highs and record lows. We do not. This is far more consistent with an increasing mean.
Dan H., The models are part of the science.
Sorry, I thought you were trying to change the subject.
With regards your points. We can leave point 2 as we agree on that.
I can see what you mean by saying that something is changing to make high sigma events happen more often and that this means there is a problem with the model of a normal distribution. However what is changing is the warming trend. As Tamino has pointed out this warming trend increases the likelihood of 3 and 4 sigma events. As the Hansen paper does, you can choose various solutions to this; use the earlier sigma before the warming trend, use sigma from a detrended data set, use sigma from the most recent period. All of these are valid approaches provided it is clear what is being done. As I said in my blog post – I preferred to present the images that use the 1951-80 sigma precisely because I was interested in the changes since that period.
To claim that the model of a normal distribution is wrong is to ‘throw the baby out with the bathwater’. The change in the proportion of events within different SD demarcations is an important observation, not just a statistical artefact. Yes, the sigma is changing, but it is an important change with real effects in terms of people’s every-day lives, i.e. 10% of the planet’s surface is experiencing 3 sigma warming in summer (using the 1981-2010 detrended temperatures to derive sigma). That is not a result of the model being wrong, it’s a result of warming.
Oops!
My above post was directed to Norm Hull.
More on weather extremes:
From Princeton’s press release (emphasis added):
Ray from 135,
If you define extreme as a record high and low for a place, certainly your are correct in your analysis. You will also have hundreds of thousands of extremes each decade just in the united states.
http://www2.ucar.edu/news/1036/record-high-temperatures-far-outpace-record-lows-across-us
For those that have an extreme definition that chooses weather events that are not as prevelent, it is important to model them correctly. The length of time that it was hot, the lack of rain, the deaths, the wild fires, the crop losses all might be considered in a model that defines what made the Russian Heat Wave an extreme event.
Chris R from 137,
I think part of the problem is definition of terms. If 10% of the planet is now experiencing 3 sigma temperatures, I think you must agree that the odds of our model being correct are not good.
So let us rephrase, to 10% is experiencing what was calculated to be 3 sigma from a previous temperature distribution. Then their is an implied judgement that this is a bad thing. Now if that distribution was from the coldest of the little ice age, it may be good, and not extreme at all in historical context. But let us not look at good or bad, and in the case of the Russian heat wave, let us agree on the bad (fires, crop failures, death), only the science.
If you define extreme as 3 SD hotter or colder than some fixed date, then we can certainly determine the areas that follow this definition between that date and now. This is what Hansen et al. has attempted to do, and we can look at the maps created. I think we both agree to this.
Now there seems to be attribution associated and the idea that these marks are independently 3 sigma. This is where I disagree. To properly test the model the distribution must be tested using the mean from that year. To test attribution the probabilities must be determined from a model without this factor. Let’s say you did this and found under the better modeling the odds were 300:1 instead of 1000:1, I would still say that it is occurring more often then the model. If it was indeed 30:1 instead of 1000:1 then indeed this shifting mean could explain the phenomena. This work needs to be done, and if attribution is important climate change must be separated from climate variability. I do not know what the real number are, but the work should be done if we are to have a good model.
Now
Norm
There is no implied judgement that this is a bad thing. That judgement is from reasoning aside from the bare observations and the statistical measures obtained from them. Many people here in the UK would love to have more ‘barbecue summers’ – their judgment would vary wildly from mine.
Because of interannual variations in weather it is meaningless to use the SD of a particular year. All the more so if one uses the SD of a year with a 3 sigma event.
I remain wholly unimpressed by your claims of model failure. As I have said above; the basic premise is testable in Excel. To avoid the extra pages involved in making sets of normally distributed random numbers I have used the Data Analysis add-on and it’s relevant function. Then the histogram function allows building of the histograms. Even with an SD of 0.5 and a slope incrementing in 1/1000 for a set of 256 numbers the skewing of the histogram is obvious, as is the increase in high SD events (random numbers).
Now Hansen shows the same thing as is found by an amateur armed with a spreadsheet. Barriopedro figure 2 also impicitly shows the same skewing at work.
The ‘model’ of a normal distribution isn’t broken. We are seeing the distribution skewed by an increase in mean temperatures. If you think there’s a problem the ball is in your court.
GISS station data is available here:
http://data.giss.nasa.gov/gistemp/station_data/
“The ‘model’ of a normal distribution isn’t broken. We are seeing the distribution skewed by an increase in mean temperatures. If you think there’s a problem the ball is in your court.”
I definitely think climate data does not follow a normal distribution only skewed by global warming. My claim was only, that you need to recalculate your distribution and test the hypothesis and not just assume it is correct. There definitely were a great deal of “extreme events” in the 1930s.
It is you that wants to lock the distribution in time. I think this is fine if that is your definition of extreme events. It does not stop the responsibility to test the model. Stephan says he is testing his model with a great deal of data sets and I look forward to see how well it predicts. My gut feel from historical records is that the variation does not follow a gausian distribution, but is skewed.
Chris R said
Because of interannual variations in weather it is meaningless to use the SD of a particular year. All the more so if one uses the SD of a year with a 3 sigma event.
I said about the mean for that year, meaning the trend line. If you are saying all the skew is related to warming, I am saying, go ahead model the warming and see what your model predicts. Is that clearer? You obviously are picking the 3 SD from some model year that is previous to today.
Even with an SD of 0.5 and a slope incrementing in 1/1000 for a set of 256 numbers the skewing of the histogram is obvious, as is the increase in high SD events (random numbers).
Now Hansen shows the same thing as is found by an amateur armed with a spreadsheet. Barriopedro figure 2 also impicitly shows the same skewing at work.
ah, but you are giving it a model and then saying it tests to your model. I am saying that you need to test the skew with a model and see the probabilities. Hanson has not done this. Stephan says he is in the process of peer review on his test, and I am very curious if he will test the variation.
In a true Gaussian distribution, and increasing mean should result in increased probability of high sigma events. A look at US record high temperatures over the past century+ shows that this is not the case. While the general trend exists; fewer record highs in the colder years (1880s and 1970s), and more in warmer years, the largest number of records were not set in the warmest years. More record highs were set in the 1930s and 1950s than either the 1990s or 2000s.
http://1.bp.blogspot.com/_b5jZxTCSlm0/R6O8szfAIbI/AAAAAAAAA8Y/t58hznPmTuw/s320/Statewide%2BRecord%2BHigh%2BTemperatures.JPG
[Response: Actually you are very incorrect. If you take a large enough sample (all available at NOAA) of daily records (lows, highs of max and mins), it is clear that warm records over the last decade (and even the last year) are running way ahead of low records. – gavin]
Dan, take another look at Norm’s link:
http://www2.ucar.edu/news/1036/record-high-temperatures-far-outpace-record-lows-across-us
I haven’t examined your claim that “More record highs were set in the 1930s and 1950s than either the 1990s or 2000s,” but given the relatively short instrumental record, the clearest metric is not absolute numbers of records, but the ratios of highs to lows. (Since clearly, were the series stationary–apologies if I’m misusing the stats term here!–you’d see decreasing numbers of records over time.)
And according to Norm’s link, the ratio of high to low is much more skewed toward “warm” for the 2000s than it is for the 1950s–2.04 to 1, versus 1.09 to 1.
(Sadly, it doesn’t give a similar analysis for the 30s–which, however, we all agree (AFAIK) to have been the warmest decade in the US record so far.)
I think that was the thrust of Gavin’s inline, which may have seemed a little tangential to your point, Dan–absent the ‘expansion’ I’ve tried to sketch in this comment.
Oh, I should mention that the graph linked in #145 is unreadably small for me–as usual, trying to zoom in just resulted in a bigger blur. The curve is clear enough, but reading the labels on the axes was just a lost cause.
Kevin,
The graph to which Norm linked is a 100% stacked column, which compares the highs to the lows in a given column. No reference can be made to other columns. Both the UCAR report and NOAA (as Gavin states) relates the relative number of highs and lows, and not absolute numbers. By comparison, more record highs were set in the 30s and 50s, but the number of record lows were much higher in those decades, so the ratio of highs to lows is less. That is what the graph shows.
The recent warming would be reflected in the ratio of record highs to lows, and indeed it is. However, the claims of increasing extremes with an increasing mean is not. The high sigma events of the 30s (and 50s) would still be considered high sigma today. The mean has not increased enough for for these extreme events to fall within the 3 sigma region.
Dan H. is arguing about his interpretation of one blurry picture.
Gavin’s response above to Dan begins “Actually you are very incorrect.”
That’s somehow reminiscent of what Tamino said to Dan earlier.
There’s a pattern here.
Dan. H should have read the caption to the picture he’s describing.
Norm Hull,
The 1930s are irrelevant. We’re talking about the recent warming, the global mean of which is attributable to human activity, i.e. post 1975 – the start of the recent linear trend. Studying the 20th century may well reveal skewing in different directions. However the recent warming trend is atypical of the global temperature behaviour in the 20th century. The 1930s warming was primarily a far-northern pattern probably related to the AMO, an outcome of internal ocean/atmosphere variability. What evidence do you have of more extreme events in the 1930s?
No. In my amateur experiments in Excel I’m testing an artifical dataset that I know to be of a normal distribution with a prescribed trend – that shows the same sort of skew to the normal distribution that Hansen finds in real results. Furthermore this is a trivial observation – the skewing of the normal distribution in a series containing a trend is well known in statistics.
I do not want to lock the distribution in time: I have previously stated that Hansen’s use of three sigmas, two over different periods and one using detrended data for the most recent period, is fine. That these three tests show a consistent pattern of skewing of the distribution and the decadal advance of this skewing is conclusive evidence that the change in the distribution is due to the trend.