A few months ago a paper by Jim Houston and Bob Dean in the Journal of Coastal Research (JCR) cast doubt on whether global sea level rise has accelerated over the past century or so. As things go these days, ‘climate sceptics’ websites immediately heralded this as a “bombshell”. A rebuttal by myself and Martin Vermeer has now been published in JCR.
The keystone of the argument by Houston & Dean is the fact that a prominent global sea level reconstruction (Church & White 2006) shows no acceleration since 1930. Which raises the question: why 1930, given the sea level data set starts in 1870? The reason becomes immediately evident when looking at the acceleration starting from any arbitrary date (Fig. 1).
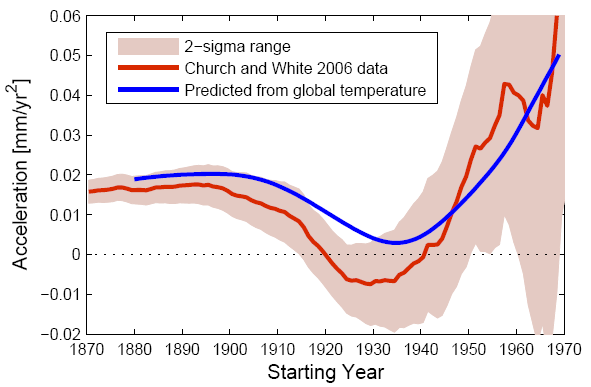
Figure 1. Acceleration of sea-level rise (i.e., twice the quadratic coefficient) from different starting years up to 2001 in the global tide gauge data set of Church and White (2006; red line with uncertainty band). Note that after ~1960 the calculation gets excessively ‘noisy’ because the time interval gets too short to robustly compute acceleration. I graphed this right away after reading the Houston & Dean paper, and a few days later Tamino independently came up with a similar plot – it’s the obvious thing to do. The blue line shows the same quantity from the sea-level hindcast of Vermeer & Rahmstorf (2009) computed from global temperature data.
Around 1930 we see a unique minimum in the acceleration curve – I will explain the cause of this shortly. Other start dates either before or after this minimum show positive acceleration. Picking 1930 for this analysis is thus a classic cherry-pick, and according to the authors that is no accident. They write in the paper: ‘Since the worldwide data of Church and White (2006)…appear to have a linear rise since around 1930, we analyzed the period 1930 to 2010.’ The interval was thus hand-picked to show a linear rise rather than acceleration.
Connection to temperature
Houston & Dean use their result to question the future acceleration of sea level rise predicted by Vermeer & Rahmstorf (2009) for the 21st Century as a consequence of global warming. They argue that the 1930s acceleration minimum calls into question the semi-empirical link between global temperature and global sea level proposed by us in that paper. However, it is clear they never bothered to check this, because quite the opposite is the case: our semi-empirical formula predicts this acceleration minimum, as the graph above shows. As it turns out, this is an expected outcome of the mid-20th-Century plateau in global temperature.
If one subtracts out the non-climatic sea level change due to water stored in artificial reservoirs on land, as we did in Vermeer & Rahmstorf (2009), then the agreement between the acceleration curve predicted from global temperature with the actually observed curve is even better (graph below). Thus, the 1930s acceleration minimum pointed out by Houston & Dean supports our approach and projections rather than challenging them.
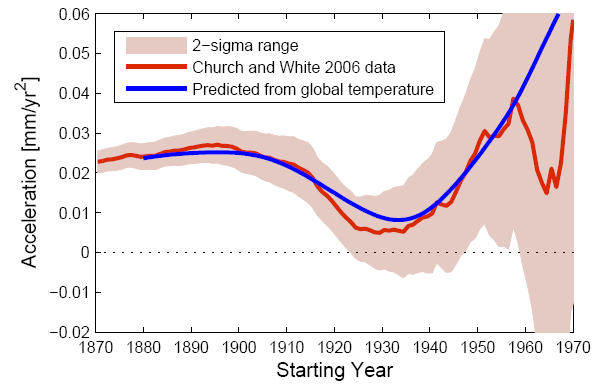
Figure 2. The same as Figure 1, but here the sea-level data are corrected for water storage in artificial reservoirs (Chao, Wu, and Li, 2008).
Regarding our projections of future sea level rise, Houston & Dean write:
it is not clear that the acceleration necessary to achieve these comparatively large projected rises in mean sea level over the course of the 21st century is evident in tide-gauge records.
That is a puzzling statement. Why would the acceleration we expect only for the 21st Century already show up in tide gauge records of the 20th? Since we expect a temperature rise to cause an acceleration of sea level rise, the acceleration in the 20th Century (which has seen only 0.7 ºC of global warming) must obviously be much smaller than that expected for the 21st Century, for scenarios of a many times greater warming.
Further issues raised by Houston & Dean
Houston and Dean raise a number of further points (beyond the Church & White global data set) on which we just cite the brief summary statements and refer the readers to our journal comment for more detail:
- Many U.S. tide gauges show a deceleration; since 1930, most of them do.
However, again, 1930 is a special choice, and U.S. tide gauges only provide a regional signal, not a global one.
- The authors’ extension of the Douglas (1992) sea-level compilation shows a sea-level deceleration for 1905–2010.
But this data set is not a properly area-weighted global average but is instead highly biased to the Northern Hemisphere. It is known that the twentieth-century acceleration is largely found in the Southern Hemisphere (Merrifield, Merrifield, and Mitchum, 2009), and the only two Southern Hemisphere groups in the extended Douglas data set indeed show acceleration.
- Decadal trends in tide gauge compilations show large variations over the full record, and the most recent decadal trends are not unusual.
However, these variations in decadal tide gauge trends are not a climate signal but rather are dominated by sampling noise due to the inadequate number of tide gauges.
- The satellite altimeter record shows a slight deceleration since 1993.
But this time interval is far too short to draw any conclusions.
In our comment we conclude:
None of this supports a lack of acceleration in global sea-level rise, as compared to what is expected from global warming. Outside a few starting years around 1930, global sea-level reconstructions robustly show a modern acceleration of sea-level rise in conjunction with global warming.
For the evidence, just have a look at some of the references listed below.
p.s. I just see that JCR also carries a reply by Houston & Dean to our comment. This largely focuses on our supposedly “selective” use of data, because we show the acceleration of sea level rise ‘only’ for starting years from 1870 (the start of the data set) to 1970 (after which the computation is too noisy to be meaningful by anyone’s standard). This is slightly ironic given that Houston & Dean focused only on the rather unique start year 1930. Houston and Dean further argue that the data already become too noisy around 1940 because “decadal fluctuations begin to dominate records shorter than about 60 years, and accelerations become increasingly meaningless for starting years in Figure 1 greater than about 1940”. We disagree: while this may be true for individual records it is not true for the global sea level reconstruction shown. The 2-sigma range and the fact that the curve is smooth until then shows it is meaningful up to about 1960; we continued the graph up to 1970 in order to show (rather than just claim in the text) how the uncertainty explodes after 1960. In any case, by showing the plot until 1970, we allow readers to see the full potentially meaningful range and judge for themselves whether they see any significant difference between the data and our model. That our model is somehow called into question by the observed sea level acceleration was, after all, a key claim in Houston & Dean’s original paper.
Houston & Dean excuse the strong northern-hemisphere bias introduced by their simple averaging by saying that “this criticism would apply to any study of sea-level rise”. That is not true; the sea level data set we use (Church and White 2006) and also the temperatures (GISS) use an area-weighted averaging scheme that makes sure the northern and southern hemispheres are properly represented in proportion to their surface areas, regardless of the data density.
But at least on one thing we agree. As Houston & Dean state in their final sentence, we indeed predict a much larger acceleration of sea level rise in the 21st Century than is observed in the 20th Century. That is a direct logical consequence of the fact that we expect much larger warming in the 21st than in the 20th.
Update 24 July: A related case of “lack of acceleration” – also from the Journal of Coastal Research – is expertly treated by Tamino here: How Not to Analyze Tide Gauge Data. It does raise some questions about the quality of peer review at JCR.
Link
References
Church, J. A., N. J. White, 2006: A 20th century acceleration in global sea-level rise. Geophysical Research Letters, 33, L01602.
Douglas, B. C., 1992: Global sea level acceleration. journal of Geophysical Research-Oceans, 97, 12699-12706.
Houston, J., R. Dean, 2011: Sea-level acceleration based on US tide gauges and extensions of previous global-gauge analysis. Journal of Coastal Research.
Merrifield, M. A., S. T. Merrifield, and G. T. Mitchum, 2009: An Anomalous Recent Acceleration of Global Sea Level Rise. Journal of Climate, 22, 5772-5781.
Rahmstorf, S. and M. Vermeer, 2011: Discussion of: Houston, J.R. and Dean, R.G., 2011. Sea-Level Acceleration Based on U.S. Tide Gauges and Extensions of Previous Global-Gauge Analyses. Journal of Coastal Research 27, 784–787.
Vermeer, M., S. Rahmstorf, 2009: Global Sea Level Linked to Global Temperature. Proceedings of the National Academy of Science of the USA, 106, 21527-21532.
Uh, didn’t part the earth’s diameter just melt away? Ice cube trays?
> day length
Try Scholar, not Daly, if you’re looking for science papers.
At least take that page’s cites and look for subsequent more recent references.
Don’t assume the planet is a uniform solid, either.
Ever played with a gyroscope?
http://onlinelibrary.wiley.com/doi/10.1111/j.1365-246X.2004.02510.x/full
ps, anyone know of anything more recent along this line?
http://www.sciencemag.org/content/297/5582/831.short
Science 2 August 2002:
Vol. 297 no. 5582 pp. 831-833
DOI: 10.1126/science.1072188
Detection of a Large-Scale Mass Redistribution in the Terrestrial System Since 1998
148 Scottie said about changes in earth’s rate of rotation.
If you can calculate all the stuff you said you could calculate why didn’t you calculate the change in the earth’s moment of inertia due to a 3mm/year sea level rise? To make it easy, assume that all that rise is due to thermal expansion of the oceans. The oceans are about 1/10^4 of Earth’s mass. The annual fractional change in the earths radius due to a 3mm sea level rise is about 1/10^9 . Thus the change in the moment of inertia due to rising seas under the assumption that it is ALL thermal expansion is about 1 part in 10^13 /year. After 100 years that is a part in 10^11 change. A day is about 10^5 seconds. The change in the length of the day is thus going to be on the order of microseconds. Your graph shows millisecond time scales. With all the other noise in the system you are unlikely to be able to see this. Especially since not all of the rise increases the moment of inertia; the rise due to glacial melt would decrease the moment.
http://theconversation.edu.au/sea-levels-continue-to-rise-but-not-uniformly-csiro-2478
I think you’ll find that the length of day is increasing very slightly but it has little to do with any changes in the diameter of the earth. Rather, it is due to tidal acceleration within the Earth-Moon system.
The simple law of physics is that the Earth’s rotational velocity varies as the inverse of its radius.
A rise in sea level by 2100 of 59cm (IPCC) or 20 feet (Al Gore) would result in an easily measurable increase in length of day, and that trend ought to be detectable by now.
Does anyone here know of a length of day study where this has been confirmed – or otherwise?
Scottie, Scottie, Scottie… the formula for the moment of inertia of a sphere with changing radius does not apply. What happens is that a very thin film on the surface of the sphere gets a little thicker, an effect of an entirely different magnitude.
Here is (h/t Neil White) Walter Munk’s great paper, which should give you a feel for the magnitudes involved. Unfortunately Jerry Mitrovica’s follow-up paper is nowhere freely available, but here is a great talk by Jerry that touches upon it.
Scottie. I recommend you pick up an undergraduate physics text. There is no such law of physics as: “The simple law of physics is that the Earth’s rotational velocity varies as the inverse of its radius.” The simple law of physics that you are trying to discuss is that angular momentum is conserved: I omega = constant, where “I” is the moment of inertia and “omega” is the rotational frequency. As I pointed out above, THe change in “I” due to a 3 mm per year rise in sea level (under the assumption that the entire 3 mm comes from thermal expansion) is about one part in 10^13 and consequently, over a century the cumulative change in the length of the day would be about a microsecond. To estimate “I” as I did above we write:
I_earth = I_solidball + I_ocean
I_solidball ~= M_ball R^2
I_ocean = M_ocean R^2
where M_ball is the mass of the earth without it’s oceans) and M_ocean is the mass of the ocean. Note that M_ocean ~= M_ball/10000 . R is the earths radius. If the oceans expand an amount dR=3mm, the change in I_earth will be due to the change in I_ocean, not in the solidball part. If the ocean’s expand dR, the new moment becomes:
I_earth = M_ball R^2 + M_ocean (R+dR)^2 ~ = M_ball R^2 + M_ocean (R^2 + 2 R dR)
Note that the solidball contribution to I_earth does not change. This is why your argument fails Scottie.
The fractional change due to the ocean expansion compared to the total is
2 dR/R M_ocean/M_ball ~= 1/10^13. After a century this would result in a change in the length of the day of about a millionth of a second. Given all the other sources of the change in the length of the day this is not observable.
Scottie: Al Gore’s 20 feet figure is not related to any specific time-frame.
The thing about sea level rise is that we are very uncertain about how fast it will happen, but we can be absolutely sure that it will happen. It’s basic physics.
If you wish to persist with your “it’s not rising” idea, then please will you calculate for us what change to the day length you expect to see for the currently observed sea level rise?
“A rise in sea level by 2100 of 59cm (IPCC) or 20 feet (Al Gore)”
Nowhere does Gore say that sea level will rise by 20 feet by 2100. He never put a date on it, only that it would happen if the Greenland ice sheet and the West Antarctic ice sheet melted. And, as Martin points out in #157, there would be no detectable change in length of day.
> rise in sea level by 2100 of … 20 feet (Al Gore)
Scottie, that’s bogus.
You’re rebunking a claim widely circulated years ago. Some guy calling himself “joeduck” was the last one I remember still posting it here, til you.
You can do better than wherever you’re getting your bad information.
Look it up. I did:
https://www.realclimate.org/?comments_popup=640&rcommentid=109805#comment-109699
157, MartinVermeer: What happens is that a very thin film on the surface of the sphere gets a little thicker, an effect of an entirely different magnitude.
And it gets less dense at the same time, further reducing the effect.
Hi, the thermal expansion leads to only a very, very small increase of I_earth as shown above. This is due that only the ocean water expands but not the inner of earth.
But the the increase of I_earth due to the melting land based ice near the rotational axis and the redistribution of melt water into the ocean is much greater, and has been already measured, see
http://www.skepticalscience.com/Bulging-at-the-waist.html
John E. Pearson #158, a good order-of-magnitude estimate, but in fact it’s a little more complicated. First of all you assume that the ocean expands homogenically, i.e., the whole ocean mass moves outward from R to R + dR. In reality of course the bottom of the ocean remains in place and so does the water touching it, so the mean movement of the ocean is only half of this, R -> R + dR/2.
…but not even this is enough: a large part of the actual thermal expansion takes place mostly in a rather thin tropical surface layer, not the full ocean depth. And we haven’t yet talked about horizontal (latitudinal) water movements…
Looking at melting ice sheets, you get much bigger effects. This is because actually (to first order) M_ocean changes; by a fractional amount of dR/D, where D is mean ocean depth.
I find that a relative change in rotation rate of this magnitude gives, for a day ~= 10^5 s, 1/10^8 s or 10 nanoseconds in length-of-day. After a century (~40,000 days) it builds up to 0.4 ms. The ice sheet effect would be a factor ~1000 larger, order 0.01 ms in LOD, cumulating to 0.4 s. A tall order to detect, but this is for 3 mm only.
Well the 2nd reply to H&D is now open access as well as a 2nd H&D reply, also a 2nd H&D JCR paper is now open access and deals with the 18.6 year lunar nodal tide and its potential effects on SINGLE tide gage records of varying record lengths;
http://www.jcronline.org/toc/coas/0/0
http://www.jcronline.org/doi/pdf/10.2112/JCOASTRES-D-11-00098.1
http://www.jcronline.org/doi/pdf/10.2112/11A-00010.1
http://www.jcronline.org/doi/pdf/10.2112/JCOASTRES-D-11-00045.1
It would appear that H&D seem only concerned with the past up to the present day, but are not willing, at all, to consider other data sources or future outcomes of a warming climate in the 21st century. Go figure.
However, H&D do finally admit the existence of Church & White (2011) that RV mentioned in their earlier reply, but only in passing and very briefly, with this cherry picked quote;
“Church and White (2011) note that the rise measured by the altimeters is not statistically different than peaks in trend in the 1940s and 1970s.”
Give me a break H&D, put both of your JCR papers next to Church & White (2011), it’s like Amateur Night at the Apollo, by comparison.
AFAIK, the 18.6 year nodal tide has little to no effect on area weighted global estimates of SLR using all available tide gages and altimetry data available for making said GLOBAL estimates of SLR. But, I’ll gladly stand corrected if this is shown not to be the case.
MArtin, DOesn’t the ice sheet stuff go the wrong way? Anything that flows into the ocean decreases the moment of inertia rather than increases it. That’s why I ignored it, besides it being complicated. I have no idea as to whether the sign of the overall change is even positive. I think a microsecond per century is a decent upper bound, no?
I am particularly grateful to Neil White (#150) for pointing me towards Walter Munk’s excellent paper “Twentieth century sea level: An enigma”. This is exactly the sort of thing I was hoping to find.
I see no point in engaging with those commenters who deny the laws of Kepler and Newton, nor will I be side-tracked by responding to condescending remarks, but thanks to everyone else for your responses. And yes I agree, let’s forget about Al Gore. He is a bit of an embarrassment!
Briefly:
[My bold throughout]
Munk starts by outlining a problem with estimates of current sea-level rise, and one of the constraints on one possible explanation is that “severe limits are imposed by the observed perturbations in Earth rotation.”
And concludes:
So it would appear that variations in the Earth’s rotation are very much a part of the equation. Now we need to know whether any sustained increase in LOD has been observed in recent years, as this could be an indication of accelerating sea-level rise. This is a fascinating subject.
If anyone knows of more recent papers, I would be very interested in reading them.
Scottie (#167)
For a start you could try looking at the other two papers I referred to in my earlier post. They are both more recent, and the Mitrovica et al paper largely resolves Munk’s “enigma”.
> forget about … Al Gore… embarrassment!
You got bad info, copypasted it, and blamed him — so that is your embarrassment, not his. Spinning it as not your problem is another mistake.
So, where did you get your bad information?
What was your source for that claim?
It’s no shame to be fooled once.
But it will help to know where you got fooled and why you trusted them.
Seriously, if you don’t know how to check the stuff you read, and you’re getting old information but not current info — that’s part of the problem and a good place to start.
John #166, nö it goes the right way: ice from close to the rotation axis (polar ice sheets) goes to all around the Earth i.e. farther from the rotation axis on average.
It’s the distance from the rotation axis that counts for the moment of inertia, not the distance from the Earth’s centre.
Scottie, here a freely readable copy of the Mitrovica et al. 2006 paper. Thanks to Archie Paulson, in spite of himself…
What Neil White said.
170: John slaps himself in the forehead.
Hope this is not OT
The ‘sceptics’ have now moved onto to a paper that they say claims that sea levels started rising before 1800 (Jevrejeva, S., J. C. Moore, A. Grinsted, and P. L. Woodworth (2008), Recent global sea level acceleration started over 200 years ago?, Geophys. Res. Lett., 35, L08715, doi:10.1029/2008GL033611. and Jevrejeva, S., A. Grinsted, J. C. Moore, and S. Holgate (2006), Nonlinear trends and multiyear cycles in sea level records, J. Geophys. Res., 111).
The authors apparently used data tidal gauges in Amsterdam, Liverpool and Stockholm.
The ‘sceptics’ are using this to claim sea level rises started before industrialisation could’ve had an effect.
Any comments or suggestions? It could be that the ‘sceptics’ just switch attention fast.
PS. I’m not going to give the ‘sceptic’ website as I don’t feel obliged to help them with any advertsing beyond the above…. unless people here want it
My thanks to Martin Vermeer (#172) – I do appreciate your guidance in finding the Mitrovica et al. 2006 paper. I’ve also found time to study the Munk paper, postings and comments here at RC – and papers by Nils-Axel Mörner (yes, I know!)
Complex as the understanding of interchange of angular momentum between the Earth’s core, lithosphere, hydrosphere and atmosphere over geological time scales undoubtedly is, I still come back to my initial simple observation that: “as the diameter [of the planet] increases, the rate of rotation will slow in order to conserve angular momentum.”
Both Munk and Mörner suggest that thermal expansion of the oceans is a less important factor in sea-level rise, especially over short/medium time-scales. But the proposition is that sea-levels are rising, and the rate is accelerating. What could be the reason?
Well, melting polar ice must be a prime candidate. Munk suggests:
Martin Vermeer (#171) makes a very similar point in response to John E. Pearson (#167)
Modern apparatus such as an atom interferometer gyroscope can measure the Earth’s rotation with an accuracy great enough to confirm Einstein’s general relativity, so detecting an increase in LOD of around 0.1ms or even an order of magnitude less should be a walk in the park. Has this been detected, and if not what is the explanation?
Finally, for the tetchier commenters here, please be assured that my comments are not motivated by anything other than a desire to understand the science behind current sea-level rise.
> Has this been detected, and if not what is the explanation?
Scottie, there are many other things that affect the Earth rotation on much shorter than geological time scales: tidal friction from Sun and Moon, and variations in angular momentum of the non-solid components of the Earth, like atmosphere and ocean. The only way to remove these, and find the “clean” change in LOD due to moment-of-inertia change, is by modelling them. And while this modelling is pretty good, it is not perfect. Yes, there are great technologies nowadays for measuring Earth rotation, but this is a fundamental limitation the battle against which is uphill. That being said, as the Munk and Mitrovica papers show, 20th century sea-level rise actually shows up in this data.
Now, as we are really interested in the moment of inertia, there is another technique: monitor the dynamic form factor J2 of the Earth’s gravitational field (which is related to the moment of inertia around the rotation axis) directly using laser ranging to satellites, as was referred to by Uli.
BTW Mörner’s papers from before the sad mystery event may well be OK :-)
Has anyone taken a look at “SteveF”‘s attempt to “improve” on V&R 2009 over at the Blackboard?
(I’m not sure whether this steveF is the same person as Steve Fitzpatrick)
#174, Jeremy C – Jevrejeva 2008 is a tide gauge sea level study reaching back to 1700. They fit a polynomial curve to the resulting record and find the lowest point (trough) occurs at around 1770, hence ‘accelerating for over 200 years’.
However, there is only one tide gauge station before 1768 and only three before ~1850, all situated in North-Western Europe. Given the lack of spatial diversity the small upward trend in the record before 1850 could easily be regional rather than global.
The recent Kemp et al. 2011 paper shows a comparison chart featuring various paleo-sea level data. Some of these do corroborate the idea of the uptrend beginning in the early nineteenth century but again the data is quite spatially-homogenous.
It’s plausible but really the trend is quite small up until the mid-to-late nineteenth century however you look at it.
Thanks for all the suggestions for my reading list!
I have now studied (amongst others) papers by Nerem and Wahr (2011) and by Botai and Combink (2009), also the recent paper by Zwally & Giovinetto (2011), who challenge some assumptions and identify the uncertainties inherent in the three techniques used to estimate polar ice loss. Their re-analysis puts ice loss from Antarctica at the lower end of most current estimates.
As to Length of Day, Landerer, Jungclaus & Marotzke (2007) calculate that “ocean warming and the ensuing mass redistribution change the length-of-day by −0.12 ms within 200 years.”
For anyone interested in possible changes in LOD due to sea-level rise, the IERS site holds invaluable records and easy to understand descriptions of the various factors affecting the Earth’s rotation.
Scottie: I don’t really think anyone is going to wait 200 years in order to see whether they can measure and correctly attribute a -0.12 ms change in LOD.
I think we will just have to make do with those direct measurements of sea level we have instead.
Didactylos: Well, for reliable direct measurements you’d obviously need a method that does not suffer from:
Mechanical errors;
Clock errors;
Calibration errors;
Datum errors;
Analysis errors;
And that preferably does not require adjustments for glacial isostatic adjustment.
Measuring an increase in LOD would appear to tick all the boxes, and if sea-level rise is accelerating, you might have to wait a lot less than 200 years to detect a signal ;–)
Scottie, did you keep looking after you found that one?
If so, did you find this one too?
http://www.ingentaconnect.com/content/igsoc/jog/2011/00000057/00000201/art00009
Greenland ice sheet mass balance: distribution of increased mass loss with climate warming; 2003-07 versus 1992-2002
Authors: Zwally et al.
“… The net balance changed from a small loss of 7 ± 3 Gt a-1 in the 1990s to 171 ± 4 Gt a-1 for 2003-07, contributing 0.5 mm a-1 to recent global sea-level rise….”
Hank Roberts (#182): Yes thanks, I did see that paper. It seems to agree broadly with other estimates of Greenland ice loss. It seems that although the Greenland ice sheet is gaining mass inland, it is losing mass round the coasts, resulting in a net loss.
But I found the the Zwally and Giovinetto paper particularly interesting because of its attempts to identify and quantify the uncertainties.
Don’t you?
Scottie #181
> And that preferably does not require adjustments for glacial isostatic adjustment.
But it does…
The real problem though is the disentanglement from the effects of atmospheric angular momentum variations and lunisolar ocean tidal friction, which require disgustingly detailed modelling… no way is this a clean observable. And VLBI is already a very good direct technique.
Sorry for my sloppy terminology. When responding to Didactylos’s comment about “direct measurements” I confess I was thinking of tide gauges. Of course GIA must be corrected for in LOD measurements, but isn’t that a global correction, unlike the individual local corrections for each and every tide gauge. I mean, would the GIA correction for a tide gauge in (say) Iceland be the same as that for one in (say) Hong Kong? Could this be a source of error or uncertainty?. Or have I got this completely wrong?
According to IERS, many irregularities of the Earth’s rotation are already well understood, e.g. Polar Motion (Chandler wobble), Celestial motion of the pole, variations due to the zonal tides, atmospheric circulation, internal effects and the transfer of angular momentum to the Moon orbital motion.
Is it really so difficult to detect the expected increase in LOD due to sea-level rise? Perhaps it is.
In a 2007 interview by EIR, Dr. Nils-Axel Mörner (yes, I know) said about sea level rise:
What are we to make of all this?
> IERS
Use the search tool on their page; search for “ice cap”
http://www.iers.org/nn_10910/sid_5123E1DE255B03D33BCBD54800D8562D/SharedDocs/Publikationen/EN/IERS/Publications/tn/TechnNote30/tn30__139,templateId=raw,property=publicationFile.pdf/tn30_139.pdf
> EIR
Larouche’s “Executive Intelligence Review” — consider the context.
> What are we to make of all this?
The “matter of physics” you quote is a claim about looking for a detectable change in the rotation rate of the planet — discussed above; not detectable in the noise. See the IERS link.
So, let’s see, a decrease in LOD of 0.12ms over a time span of 200 years works out to -0.6 µs/yr (on average).
So, should I plot this as a linear trend or a quadratic trend?
I would guess quadratic IF the resulting quadratic trend line were actually observable (measurable) in nature.
If all of this is assumed to be purely quadratic (e. g. deceleration), we’d start out at a rate of 0.0 µs/yr and end up at a rate of -1.2 µs/yr (which, you guessed it, yields an average of -0.6 µs/yr).
At the 100 year mark, we would have a decrease in LOD of -30 µs and a rate of -0.6 µs/yr.
So let’s plot this one (-6 µs/yr (on average)) next to this plot;
http://www.iers.org/nn_10398/IERS/EN/Science/EarthRotation/LODplot.html?__nnn=true
Hmm, it would appear that even a purely quadratic term in LOD shows up as FLATLINED relative to other known components in LOD theoretical calculations.
I think I’ll end right aboot here.
Scottie (#185)
I suggest that you ask Nils-Axel Mörner where he gets this from. He’s retired, but still (I think) has a web site and an email address. Good Luck! If you get a coherent answer please share it with the rest of us!
I also suggest that you critically read the whole of that interview (and have a good look at the photograph of the tree).
I would guess that Mörner’s Photoshop skills have improved somewhat;
http://www.newsofinterest.tv/global_warming/effects/sea_level/morner.php
http://www.newsofinterest.tv/_sam_noitv/global_warming/effects/sea_level/morner/thumbnail_images/seaLevel_morner_large.jpg
http://www.newsofinterest.tv/_sam_noitv/global_warming/effects/sea_level/morner/morner_sea_level_not_rising.pdf (color version with different caption, still shows the “tree” as being “sawed” down though, err, I mean Photochopped ;-)
Hank Rpberts (#186) – Thanks for the link to the IERS Technical Note. It would appear that the 1998 J2 anomaly will be exercising minds for a while yet.
I am aware of the problems with Mörner’s claims. I mentioned him only because he proposed that it was definitely possible to infer sea level rise from measured changes in LOD, and claimed to have done so.
I won’t bother you again with troublesome assertions or questions. I’ve finally come across a paper which answers my original point pretty well. Landerer, Jungclaus and Marotzke (2009) propose a mechanism whereby, even in the mid range of IPCC scenarios, the small variations in Length of Day and Polar Motion induced by sea level rise, can produce small but not insignificant changes in Earth Orientation. Of course, precise Earth Orientation data are vital for spacecraft navigation, etc. The paper also suggests that Earth orientation observations can give an independent verification of global sea level rise.
> Mörner’s claims…. that it was definitely possible to infer sea level
> rise from measured changes in LOD, and claimed to have done so.
Er, he seems to have claimed he couldn’t detect sea level rise in the LOD numbers so the other measures showing it happening had to be wrong, didn’t he?
Saying he couldn’t find it isn’t saying he could measure it.
oh, dear ….
http://iopscience.iop.org/1748-9326/6/1/014004/fulltext
Effective media reporting of sea level rise projections: 1989–2009
U K Rick, M T Boykoff and R A Pielke Jr
“In order to characterize peer-reviewed literature with sea level rise projections to 2100, we completed two searches in the ISI Web of Science. The first was the Boolean search `sea’ and `level’ and `rise’, which returned 5332 articles. The second was the Boolean search of `sea’ and `level’ and `rise’ and `2100′, which returned only 107 articles. These 107 papers then became our sample for appraising the scientific literature. A large number, 76, of these papers stick to the sea level contribution from their authors’ particular expertise (e.g. thermal expansion) and time-scale (e.g. past sea level rise or current sea level rise rates), but quote the IPCC projections. These were not retained in our data set because they are not giving an independent projection. There were six papers that give sea level rise projections for a doubling of CO2 and are from the time when the IPCC was focusing on a doubling of CO2 as a metric rather than conditions in 2100. Therefore, 25 peer-reviewed papers out of the original 107 remained, to enable us to show a global sea level rise to 2100 from either one source (e.g. ice sheet melting) or all sources. The papers that included all sources of sea level rise were climate modeling studies….”