Guest post by Chris Colose (e-mail: colose-at-wisc.edu)
This post is a more technical version of Part 1, meant to quantify and expand upon some of the feedback concepts laid out previously. Additionally, the role of the water vapor feedback in planetary climate is discussed.
By convention, climate scientists define a feedback parameter, λ, to encompass the effects of the various feedback processes discussed in Part 1. In that post, it was noted that the ‘reference’ sensitivity parameter (λ0) was about 0.3 °C/(Wm-2). If we perturb the climate, this is the equilibrium temperature response (per unit forcing) that would be experienced after neglecting all feedbacks and only allow the planet to come back into radiative equilibrium. Creating this reference system (or baseline) is critical to discussing climate sensitivity, since positive and negative feedbacks are defined relative to how they modify this so-called Planck response.
The above value can be obtained by taking the derivative of the Stefan-Boltzmann equation with respect to the emission temperature (which is ~255 K on Earth).
A more realistic value of λ0 obtained in models is slightly higher than this back-of-envelope calculation (~0.3-0.31 °C/(W m-2)) due to atmospheric longwave absorption. The no feedback response is ΔT0 =λ0*RF (RF is the radiative forcing). For a doubling of CO2, which has a radiative forcing of 3.7 W m-2 in the modern atmosphere (Myhre et al 1998), one obtains an estimate of about ~1.2°C temperature change.
In the real world of course, we expect various components of the climate system to respond and further modify the temperature. This works by taking some fraction of the system output and feeding it back into the input, creating an additional term proportional to the temperature response (kiΔT for the ith feedback of interest). For n number of feedbacks, this can be formally written as (Roe, 2009),
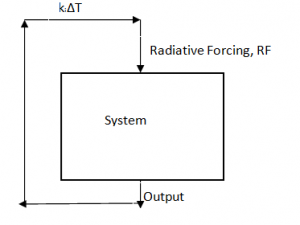
These additional terms serve to modify the initial radiative forcing, making the full perturbation dependent on the response. Each individual feedback has an associated feedback factor (f) as defined in part 1. This is proportional to the system output which is then fed back and amplifies the original forcing (f = ki*λ0). The associated climate response is
This connection between feedback factors and the final temperature response has been known for some time (see review by Roe 2009 ;Hansen et al 1984 lay out the basic mathematical framework and definitions in feedback discussions: but note the Hansen paper reverses the standard definitions of a gain and a feedback factor used in electronics, and which is used here).
The importance of the above relationship is that the climate has a non-linear response which depends on the sum of the feedback factors. For instance, with one feedback of f=1/3 the sensitivity is increased by a factor of 1.5 above the base (Planck) response. For two feedbacks of f=1/3 each, the sensitivity is increased by a factor of 3. Furthermore, the uncertainty in the temperature response due to small uncertainties in the total feedback factor depends on the true mean value of the feedback parameter.
In figure 2 note that the slope of the temperature response curve increases at higher values of f close to one. Therefore the same uncertainty in the feedback parameter range has a stronger projection on uncertainties in the response if positive feedbacks dominate over negative ones, as appears to be the case in the present day climate.

It should be kept in mind that feedbacks are, mathematically, just a Taylor Series. The often-cited divergence point to infinity as f=1 is really an artifact of assuming a linear system and ignoring higher order terms (see Zaliapin and Ghil, 2010 in discussion of the Roe and Baker work). Really, this limit corresponds to a bifurcation (loosely, a tipping point); the state on the the other side of this point could be a runaway effect or it could be just a small change in temperature.
The Water Vapor Feedback
As the globe warms from anthropogenic forcing, the water vapor feedback is the strongest amplifier of global temperature change. Despite this, some of the very popular descriptions of how water vapor feedback operates are incorrect, or at least incomplete. One rather common fallacy is to simply say “the Clausius-Clapeyron equation means warmer air will hold more water vapor” or to assert that a warmer planet must mean more evaporation, which will in turn increase the moisture content of the atmosphere.
The argument that increased evaporation is central to the water vapor feedback does not turn out to be very useful. For one thing, evaporation describes a flux of vapor from the wet surface into the atmosphere. This is a physical quantity that doesn’t have much direct relation to the amount of water vapor that is left behind, and indeed, is measured in completely different units. Evaporation (and precipitation) is also tied to the surface energy balance and depends on the wind speed and boundary layer relative humidity, so it is entirely possible for evaporation to go down in a warmer world or increase in a colder one. The surface energy balance reads as:
Ssfc is the shortwave radiation incident on the surface, weighted by the albedo α. P is the precipitation, L is the latent heat of vaporization, SH is the net upward sensible heat flux, and R is the net upward longwave radiative flux at the surface. Solar radiation absorbed at the surface is a large constraint on the amount of evaporation and precipitation that can occur. Even if you add CO2 to the atmosphere, evaporation and precipitation eventually level off even as the surface temperature increases in warm climates.
In general, evaporation and precipitation go up much less rapidly than the water vapor content, resulting in an increase of the mean residence time of water vapor in the atmosphere. This has strong implications for circulation patterns, including a weakening of the zonal (Walker) circulation and to some extent, the Hadley circulation (Held and Soden, 2006). In the warm limit, the latent heat flux is much larger than the sensible and net radiation terms, so precipitation asymptotes to a value like Pmax = S(1-alb)/L (Equation 6 in O’Gorman & Schneider, 2008), which is about 6 mm/day in the global mean.
Clausius-Clapeyron provides only an upper bound on the pressure of water vapor that can build up in a parcel of air at some temperature before it reaches saturation. This thermodynamic law says that the saturation pressure increases nearly exponentially with temperature (in the current climate, ~7% per °C). It is given in approximate form as
where A=2.53×1011 Pascals and B=5420 K (Petty,2008). However, this doesn’t tell us how or if that upper bound will be reached. For example, within the tropical high level atmosphere, conditions depart significantly from saturation.
Still further, simply adding more column integrated water vapor in the atmosphere is not enough to get a strong water vapor feedback, even if it matters for precipitation. In order to get a strong greenhouse effect you must increase the infrared opacity of the high, cold atmosphere where you can reduce the emission of longwave radiation to space. That is, water vapor will have much more impact at high altitudes than near the surface. As with CO2, the radiative effects of water vapor depend on the fractional change rather than the absolute change. Increasing the humidity of the free troposphere from 3 to 6% has nearly the same impact as increasing the humidity from 30 to 60%, so it is important to understand how the actual humidity changes at these levels scale with the upper bound set by Clausius-Clapeyron. This requires knowledge of the relative humidity distribution and how it may change in a warmer world.
Unfortunately, there are no simple constraints on the maintenance of relative humidity in the upper atmosphere (Couhert et al., 2010; Schneider et al 2010), and testing simulations of the water vapor feedback with observations is critical. In observations of seasonal variations, responses to volcanic eruptions (Soden et al 2002), ENSO, and in trends from satellites, the relative humidity tends to change very little on the global scale. This provides important evidence that the water vapor scales pretty well with Clausius-Clapeyron (Manabe and Wetherald, 1967; Held and Soden 2000; Dessler and Sherwood, 2009). This is also a result that all of the models produce fairly closely (Sherwood et al., 2010, JGR).
Understanding why this is the case is not straightforward. There is no fundamental reason that relative humidity cannot change. In the subtropics for example, relative humidity does change in twenty-first century simulations and considerably so over even broader range of climate change scenarios (O’Gorman and Schneider, 2008).
Over the last decade, a leading framework that has emerged is that the tropospheric water vapor distribution can be quantitatively predicted by taking into account the large-scale wind and temperature fields, without the need to consider small-scale cloud microphysics. Simple models examining the statistics of water vapor ‘trajectories’ in time, and keeping track of parcel transport and saturation/condensation events, can simulate the large scale humidity fields well. In such a model, the specific humidity is determined approximately by the most recently experienced saturation value. Changes in RH owing to the change in the temperature of last saturation are quite small in the present-day climate (e.g., Pierrehumbert et al., 2007 Equation 6-19; see also Pierrehumbert and Roca 1998; Dessler and Minschwaner 2007; Sherwood et al., 2010; Reviews of Geophysics).
In addition to the direct radiative impacts discussed above, the water vapor distribution is tied to various cloud feedbacks that may occur in a changing climate. For instance, the troposphere is heated by convection only where it is cooled down by radiation. The profile of tropospheric infrared cooling is expected to shift upward in a warmer world primarily due to the increase in upper level humidity. It follows that the vertical extent of convective overturning should increase and the temperature at the tops of tropical anvil clouds should remain about the same during climate change, which would decouple the emission temperature from the surface temperature (Hartmann and Larson, 2002). This could be a mechanism by which virtually all models tend to simulate positive longwave feedbacks (Zelinka and Hartmann, 2010). The bulk of uncertainty behind the cloud feedback actually comes from the shortwave component, which is dominated by low clouds that have a high albedo.
The Runaway Greenhouse
The simplest energy balance model that provides a boundary condition which constrains the climate of all Earth-like planets is obtained by equating the absorbed solar radiation with the outgoing terrestrial radiation.
What water vapor does as a greenhouse gas is to smooth out the outgoing radiation curve as a function of temperature, making it more linear than the T4 Stefan-Boltzmann dependence. Just as with CO2, water vapor makes the atmosphere a poorer emitter of radiation to space and enhances the surface temperature (Figure 3) .
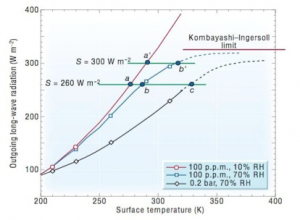
The water vapor feedback in this diagram can thought of as the warming difference between b’-b and a’-a, where the prime terms are the new climate state as the solar radiation is increased. In other words, the range of temperature change becomes larger for similar changes in the OLR for a planet with higher relative humidity.
The extreme warm end of a feedback scenario, popularly known as the runaway greenhouse, can arise when the atmosphere is composed of a greenhouse gas that is in vapor pressure equilibrium with a large, surface volatile reservoir. When you add greenhouse gases to the atmosphere, warm surface emission is preferentially replaced by emission from high, cold regions of the atmosphere. Since the water vapor feedback means the IR opacity is dependent on the temperature itself, eventually the emission to space can be decoupled from the surface temperature completely.
As the specific humidity continues to climb, the limiting infrared cooling that can occur for a planet comes at a threshold known as the Simpson-Kombayasi-Ingersoll (SKI) limit. If the incoming absorbed solar radiation exceeds this radiation threshold then the surface temperature must rise until the oceans are either depleted or the body becomes hot enough to radiate in significantly shorter wavelengths to which the air is rather transparent. The SKI limit therefore sets the inner edge of the habitable zone (where a planet can evolve with liquid water). This standard scenario is very important for understanding the evolution of other climates (in particular Venus, or exoplanets close to their host star). The runaway greenhouse scenario is likely the harsh fate Earth will encounter in the geologically distant future, as the sun gradually brightens over time.
Contrary to some popular impressions, CO2 plays only a very small role in setting the limit at which a runaway greenhouse is obtained. Once an ocean’s worth of vapor is in the atmosphere, CO2 is relatively unimportant unless it exists at extreme concentrations. One (numerically) calculated upper limit on the outgoing radiation for a planet with Earth’s gravity is about 309 W m-2 or about 1.4 times the modern solar constant, noting that the albedo of an H2O atmosphere is higher than the modern case (Kasting, 1988).
In conclusion, water vapor is the dominant feedback on our planet and is also important for understanding the evolution of planetary climate. Observations and models support a roughly 7% increase in specific humidity per degree warming, consistent with scaling of the Clausius-Clapeyron relation, although the nuances of tropospheric humidity are still a topic of worthy research.
Well worth the wait! Thanks.
“As with CO2, the radiative effects of water vapor depend on the fractional change rather than the absolute change.” — But how is it actually calculated? Is there a simplified expression for the forcing from a given change in water vapor at a given altitude?
The link to “Taylor series” is malformed.
Gavin and Chris:
Usage alert: well is an adverb and good is an adjective.
“water vapor scales pretty good with…”
No need to post this comment!
[Response: ]Probably due to Norwegian editing! Fixed.–eric
Excuse me for nitpicking.
“K” of “SKI” is not “Kombayashi”, but “Komabayasi”.
The original paper is here.
Makoto Komabayasi, 1967: Discrete equilibrium temperatures of a hypothetical planet with the atmosphere and the hydrosphere of one component-two phase system under constant solar radiation. Journal of the Meteorological Society of Japan, Vol. 45, 137-139.
http://www.journalarchive.jst.go.jp/english/jnlabstract_en.php?cdjournal=jmsj1965&cdvol=45&noissue=1&startpage=137
[Response: Thanks. Fixed in the text, will fix the figure.–eric]
[Response: Ack, thanks for the corrected spelling. The mis-spelling is due to me (which I picked up from a bad transliteration years ago and have been using ever since). I have been using the Kombayashi spelling for a long time in articles, and this is the first time anybody picked up on the correct spelling; I hope I haven’t done too much damage to the fellow’s name by using the “h” spelling in my climate book; I’ll fix that in the second edition, since the thing is coming out of the presses right now. Star Trek fans have a tendency to say “Kobayashi” (as in “Kobayashi Maru,”) but I at least managed to weed out all of those. –raypierre]
Great Post! I learned a lot. It’s interesting that “Observations and models support a roughly 7% increase in specific humidity per degree warming, consistent with scaling of the Clausius-Clapeyron relation” works out so well despite the actual mechanisms being much more complex.
This, I think, is a key insight:
“In general, evaporation and precipitation go up much less rapidly than the water vapor content, resulting in an increase of the mean residence time of water vapor in the atmosphere. This has strong implications for circulation patterns…..”
Strong implications, indeed. It seems to me that’s where the early climate change disruptions will occur – more from changing weather patterns than the temperatures that cause them.
Lastly, Chris, you just let the cat out of the bag! What will the deniers make of:
In conclusion, water vapor is the dominant feedback on our planet
…. after having invested so much rhetoric to the effect that climate scientists ignore the most important greenhouse gas ?
Thanks for a great post.
Hello Chris!
Does the Ssfc term include near IR? On the Planck curve there is a significant amount radation of near IR just beyond the end of the visible red. Explanation of greenhouse effect usually mentions only visible light.
Is the radiation absorbed by the water droplets and cause heating of clouds?
What is the portion of water vapor transported directly from surface water by the mechanical force of the wind into the air as compared to simple evaporation? How is thus taken into account when calculating water vapor feedback? A stong wind suchas Northeaster moves larges quanities of ocean surface water onto and into the land.
What is the fate of the hot CO2and HO2 deposited in the stratopshere by really big jets? For example, a Boeing 747 takes off with 346,000 US gallons of fuel for a long international flight. Do these gases stay above the tropopause? If they do, would this lead to extra heating of the stratosphere? Or do the aerosol particles from the exhast cause cooling?
There can be no runaway greenhouse effect because in polar regions the temperature drops to low values very fast after the sun drops below the horizon. By mid to Nov the ice become at lets about 3 ft thick which allows the start of the ice road trucking season. I have been “Ice Road Trucking” on the History Channel. The amount of truck traffic on the Dalton highway at ca -30 to -40 deg C is amazing.
It’s been out for a couple of weeks, and I may have missed citations of it here, but even so it’s worth citing again:
Andrew A. Lacis, Gavin A. Schmidt, David Rind, and Reto A. Ruedy, 2010: Atmospheric CO2: Principal Control Knob Governing Earth’s Temperature. Science 15 October 2010: 356-359.
This differentiates clearly between forcing and internal feedbacks and quantifies the effects of the two quite nicely. Those results, with explanations such as the one here, may just help people understand all this better.
[Response: This short note provides a convenient and concise summary of the essentials of water vapor feedback, but it should be recognized that there is nothing there that hasn’t been said already innumerable times in various review articles on water vapor feedback, or other prior publications. In particular, the result that the Earth turns Snowball if you take out all the CO2 was published earlier by Voigt and Marotzke. See Voigt A and Marotzke J 2009: The transition from the present-day climate to a modern Snowball Earth. Climate Dynamics DOI 10.1007/s00382-009-0633-5 . Still, given all the confusion surrounding these issues they bear repeating. –raypierre]
Concerning the question of the energy of moist air (moist enthalpy): I have implemented a near-live plot showing that quantity for Diekirch, Luxembourg here.
The plot shows the sensible heat and the total moist enthalpy, the difference being the latent heat portion. A short paper describing the method can be found by following the link left of the plot (or here. The text was posted as a <a href="http://pielkeclimatesci.wordpress.com/2010/09/22/guest-weblog-calculating-moist-enthalpy-revisited-by-francis-massen/"guest post on R. Pielke’s blog.
Thanks for the spelling note Kooiti– That actually wasn’t a typo, I picked up that spelling from what other authors have written, so apparently the mistake has found its way into the literature as well. I’ve read Ingersoll’s original 1969 paper but not the one by Komabayasi, so thanks for the reference.
Taylor series, should be: http://mathworld.wolfram.com/TaylorSeries.html
So you expect people to believe what climate scientist when you can’t even understand that positive feedback = runway system.
It doesn’t mater if the positive feedback is 10x the input or .01x the input. Here is a really simple example take you bank account pretend that it gets paid 1% interest in a hundred years your bank account will still be increasing. Just like if instead of 1% it was a 101%. All that changes is the rate of change.
Now you claim that with out CO2 the earth would be really cold but CO2 alone wouldn’t warm the earth enough to support the current temps. Then it follows that adding more CO2 must have a negative feedback otherwise the planet would have long ago entered into a Venus like state.
[Response: Please try reading again, but this time without thinking that you know the answer already. Hint: positive feedback in the climate sense is not what you have assumed. – gavin]
Clear and helpful. Thank you.
Spencer @10 — A small positive feedback simply amplifies the response.
https://secure.wikimedia.org/wikipedia/en/wiki/Positive_feedback
Look it up positive feedback equals an unstable system. That grows exponentially if you don’t understand that I suggest investing in a book on control systems.
Here let me show a case for you. Assume T0 = 0 and an input of one and 10% feedback
T1 = 0 input of 1
T2 = 1 input is now 1 + .1
T3 = 2.1 input is now 1 + .21
T4 = 3.21 input is now 1 + .321
Repeat until the system equals the temperature of the sun.
[Response: If you read the post, you will see that this is *not* how this is defined for climate purposes. Rather than assume that a whole field is stupid, try and consider the possibility that terms could be defined differently in different fields. – gavin]
Spencer, at least read the “in climatology” section of the very link you provided
https://secure.wikimedia.org/wikipedia/en/wiki/Positive_feedback#In_climatology
The description is not completely right, but the very first sentence is on-target and addresses your confusion. I’ve even defined the reference system based on the Stefan-Boltzmann law in both of my posts by which climatoolgists define the “sign” of feedbacks. I’m not sure you’re reading any of this.
Spenceer @13 — From your Wikipedia link: “Electronic amplification devices may have positive feedback signal paths intentionally added …”
Now I do indeed understand linear systems theory and the correct formula, even in Chris Colose’s good expostion, is
R = (g/(1-f))F
where R is the response, g is the forward, or open loop gain, f is the feedback, constrained to be in the open interval (-1,+1) to avoid runaway or oscillation and F is the input, called a forcing in climatology. The feedback is called positive when greater than zero (imagine that!).
Here is a correctly done example in which g=1, f=1/2 and F=1:
R = (1/(1-1/2))*1 = 2
which can otherwise be understood as starting with a response of 1 and then the feedback adds a half to that and then another half of half and so on. One has
1 + 1/2 + 1/4 + 1/8 + … = 2
And, by the way, you couldn’t have read the Wikipedia article very carefully, it is clear.
Oh dear. I must learn to pause before submitting comment.
The feedback f is only constrained to be less than one; any negative amount is ok.
Thank you. Bookmarked as thermodynamics to be read again and studied. I remember as Maxwell-Boltzmann from 46 years ago. How did Stefan replace Maxwell?
I think it’s worth another comment on the Lacis et al. paper in Science, and also the related Schmidt et al paper in JGR. They both tie very much into this post. I encourage everyone to read them (they are both pretty easy reads) here and here. I also summarized their results at here on my blog.
I agree with Ray Pierrehumbert that there is nothing physically “new” or inherently surprising in the results, but in science if you don’t write it down it doesn’t count. Thus far, there has been a very weak effort to partitition the greenhouse effect by the fractional contribution between H2O, CO2, etc, and also to detail the effects of a zero ppm CO2 experiment in terms of the collapse of the water vapor greenhouse effect. I’m not sure the detailed partitioning is a very interesting scientific question, but there’s a lot of nuances behind the structure of the greenhouse effect which are still not well appreciated outside of specific expertise.
The quantiative partitioning of the terrestrial greenhouse effect shows that the contribution between various agents to the longwave absorption in the atmosphere is about 50% due to water vapor, 25% to clouds, 20% to CO2, and the rest to ozone, methane, nitrous oxide, etc. Amongst other things, this puts to rest common fallacies which claim water vapor swamps the CO2 effect. A more important implication however is that several popular claims which still show up in basic textbooks or internet descriptions, such as “water vapor is the most important greenhouse gas” or “the greenhouse effect means the surface temperature is 33 K hotter than it would be” are missing out on key feedback processes that make the respective claims meaningless.
In particular, it is CO2 (and the other non-consensable gases at Earthlike conditions) which provide the supporting framework by which the condensable component of the greenhouse effect is allowed to operate. Removing the non-condensable gases and the corresponding temperaure reduction demands that you lose most of the water vapor effect as well, further lowering temperatures, and it also means the surface albedo grows to make the total planetary albedo well in excess of the modern day 30%. Neglecting the shortwave feedback effect from the “33 K difference” relative to the modern emission temperature actually underestimates how important the trace molecules are to the climate of the Earth.
CO2 is also the most readily available forcing agent to change both fast and of sufficient magnituide to matter. Solar changes are either too small or too slow. Changes in solar distribution (e.g., Milankovitch) are slow on anthropogenic timeframes, but can probably best be served as pacemakers of climate on glacial-interglacial timescales, losing resolution or importance on geologic timeframes (particularly in ice-absent climates); CO2 (particularly as a feedback via silicate weathering) modulates Earth’s temperature, yet one can still see snowball-like planets and PETM-like situations on the way, and even these events are intimately linked to the optical characteristics of the atmosphere. There’s no way to cut corners around the physical demands of atmospheric radiative transfer, or no reason to suspect human modulation to those physics will suddenly not matter.
Edward, this will help; these are related concepts.
http://www.newworldencyclopedia.org/entry/Ludwig_Boltzmann
“In 1872, Boltzmann …. wrote an equation …. today referred to as the Maxwell-Boltzmann distribution, since Maxwell had derived a similar equation.”
…
“Stefan-Boltzmann law … established experimentally by Jožef Stefan in 1879. Boltzmann, who was Stefan’s student, successfully derived the law from theoretical considerations in 1884.”
…
… “the foundations of classical statistical mechanics…. applicable to the many phenomena that do not require quantum statistics and provide a remarkable insight into the meaning of temperature.”
Waldo #14,
There is an ongoing open thread. Would everyone with something off topic please take it there?
https://www.realclimate.org/index.php/archives/2010/10/unforced-variations-3-2/
Don’t know what impact the Spencer Braswell had in the US:
http://www.drroyspencer.com/wp-content/uploads/Spencer-Braswell-JGR-2010.pdf
However in Sweden the “sceptics” managed to get in to one of the bigger newspapers saying it showed that climate sensitivity is 0.6 C. Now that is not what it say but anyway… I think it would be grate with a post on what this kind of studies could tell us about climate sensitivity and the problems with them.
For the interested this is relevant:
http://www.citeulike.org/user/nurban/article/6976569
http://www.atmos-chem-phys.org/10/1923/2010/acp-10-1923-2010.pdf
http://journals.ametsoc.org/doi/abs/10.1175/2010JCLI3657.1
Spencer, you are taking a literal engineering view about the issue of positive feedback.
Sure engineers learn about the meaning of positive and negative feedbacks in closed loop systems, that is hardly appropriate in this context.
Language is flexible and a term in one field of endeavour can have a different meaning in a different endeavour.
It is possible that since climate science uses the term, dictionaries need to be updated to reflect a modern use. Language evolves, so there should be no reason for an update.
arrrhhh. That last post of mine should have said:
‘Language evolves, so there should be no reason for not updating dictionaries.’
Spencer @13
I’m also more familiar with electronics than climate, so I had to think through the connection for a bit before I saw what was going on. Maybe I can clarify the connection between the concepts?
Lets look at the maths from electronics. Here’s the maths for a *negative* feedback amplifier…
http://en.wikipedia.org/wiki/Negative_feedback_amplifier
We get A’ = A/(1+beta.A)
How do we turn this into a positive feedback system? Simply change the sign of beta. Then: A’ = A/(1-beta.A)
Note that if beta.A is less than 1, we still get (in the ideal case) a stable amplifier whose output does not go to infinity, but whose gain is greater than amplifier without feedback. (In practice, A tends to vary from circuit to circuit, and introducing positive feedback just amplifies the differences, so we don’t do this.)
But this seems to me to be what the climate guys are talking about with positive feedbacks. You get a bigger change in the temperature than you would expect without the feedback, but you don’t get a runaway.
Spencer wrote in comment 13:
Here let me show a case for you. Assume T0 = 0 and an input of one and 10% feedback
T1 = 0 input of 1
T2 = 1 input is now 1 + .1
T3 = 2.1 input is now 1 + .21
T4 = 3.21 input is now 1 + .321
That should have read:
Here let me show a case for you. Assume T0 = 0 and at T1 there is an input of one and 10% feedback
T0 = input of 0
T1 = 0 input of 1
T2 = 1 input is now 1 + 0.1 = 1.1
T3 = 2 input is now 1.1 + 0.01 = 1.11
T4 = 3 input is now 1.1 + 0.001 = 1.111
Tn = n input is now 10/9
Tn+1 n+1 input is now 10/9
HTH,
Cheers, Alastair.
#14 is incoherent anyway, due to ambiguous formatting–you can’t reliably distinguish between ‘waldo’ and ‘wally,’ for one thing. Moreover, the unattributed “he” abounds, meaning you often can’t tell if Gavin, McKittrick or for that matter, Santa Claus, is the intended subject. Possibly it makes some kind of sense if you have already read the papers referred to, but as it is it is practically undecipherable, IMO.
If anyone feels that the Oxford English Dictionary needs updating, you can submit a suggestion here:
http://www.oed.com/general/contacts.html#appeals
David B. Benson # 17
No !!!
Feedbacks must be in the range (-1,1).
The geometric series 1 + r + r^2 + …
converges if and only if -1 < r <1.
Otherwise it diverges.
Anybody who is a real engineer, and that excludes Spencer, knows that the climatology definition is the same as that used in the control engineering field. See the Barkhausen stability criterion.
http://en.wikipedia.org/wiki/Barkhausen_stability_criterion
I have a question for Chris – is it correct to say (and this is based on a post by Lubos Motl) that if you expand Stefan’s Law, at 192K, the quadratic term is equal to the linear term. Therefore, (and this is my opinion), at up to 20K rise, the linear feedback relationship can still be used and since burning up all fossil fuels will not cause anywhere near that range of increase, the Zaliapin/Ghil result is more of an academic curiosity that prevents the blow-up to infinity?
This is a good essay.
18, Chris Colose: I think it’s worth another comment on the Lacis et al. paper in Science, and also the related Schmidt et al paper in JGR. They both tie very much into this post. I encourage everyone to read them (they are both pretty easy reads) here and here. I also summarized their results at here on my blog.
new paragraph
I agree with Ray Pierrehumbert that there is nothing physically “new” or inherently surprising in the results, but in science if you don’t write it down it doesn’t count.
That’s well worded. I may be off-topic in asking this, but does the model used in Lacis et al provide an estimate to the lag time (“thermal inertia”) in the atmosphere system? This question can be rephrased in different ways. How long before (90% of) the full temperature effect of the CO2 accumulation to date will be experienced? For a bolus of 100ppm (say), how long before the system reaches its steady state?
Comment by Dan H. — 3 November 2011
I am a bioengineer, studying algae sequestration of carbon with the University of Illinois.
This is the problem: dissolution of atmospheric carbon dioxide occurs at the interface of atmosphere and seawater, so the drop in alkalinity & pH is greatest closest to the interface. This is also where the bulk of photosynthesis and planktonic grazing occurs.
Research is showing that calcifying phytoplankton such as coccolithophores are being inhibited by the dissolution of carbon dioxide into this interface. These phytoplankton are the foundation of the ocean’s food web, and as they are impacted, so are other important species including antarctic krill.
http://www.abc.net.au/news/stories/2010/10/13/3037651.htm
Dr. David (!) Archer seems to get this, he has a solid background in ocean biochemistry. I recommend his book “The Long Thaw” highly.
My primary concern at this time isn’t increasing temperatures but collapse of the food web in the oceans. If this happens, we better get used to eating jellyfish (a line stolen from a colleague of mine).
All further discussions of ocean pH changes should be submitted to the “Unforced Variations 3” thread. Three comments have been moved there. Keep this one on topic please.
> SM
> Lacis … thermal inertia … atmosphere
I don’t think thermal inertia is doable separately for the atmosphere, since the atmosphere’s connected to the mass of the oceans.
Here’s his Publications page:
http://pubs.giss.nasa.gov/authors/alacis.html
Re 30 (Septic Matthew), 32 (Hank Roberts), and thermal inertia. An important paper by Susan Solomon et al in last week’s PNAS explores this issue in some detail. Among the conclusions is that thermal inertia in the ocean becomes increasingly important as both the magnitude and the duration of a forcing increase, and can extend the temperature effects of a perturbation (e.g. a CO2 increase) for a very long interval after the perturbation itself has ended. The link is Persistence of Climate Change
32, Hank Roberts, If the modeling used by Lacis et al can provide the information that it provided (CO2 as control knob), it’s at least worth asking if it can provide the information that I asked for in my post.
33, Fred Moolton, thanks for the link, but I was requesting a quantitative estimate of the “time to steady state”, what in linear systems theory would be the “relaxation time” after a pulse input (but this is a question in non-linear systems theory, so analytical solutions are probably not available.)
SM, do these describe your question?
Assuming a specific limited pulse of greenhouse gas, what is
“long enough for the Earth to return
to its original temperature”?
“the time horizon for their forcing
to decay to zero and the Earth to return
to an equilibrium temperature”?
(The quotes are from the Solomon paper, thanks Fred.)
Something like this might clarify, for those with the math to read it:
NUMERICAL DYNAMICAL SYSTEMS ANALYSIS OF NONLINEAR CLIMATE MODELS
HENK A. DIJKSTRA, KURT W.A. LUST AND FRED W. WUBS (2008) – conference
http://www.iacm-eccomascongress2008.org/admin/files/fileabstract/a184.pdf
“ABSTRACT
Climate models display many interesting nonlinear phenomena …. the application of numerical techniques from dynamical systems theory (bifurcation analysis, attractor reconstruction, etc.) has shown to be very fruitful. In this symposium, we want to bring together experts on the numerical techniques used in the analysis of nonlinear dynamical systems and climate physicists….”
To continue. Figure 2 of Lacis et al (cited above) shows that, after zeroing out all non-condensing GHGs, the temperature has adjusted about 95% of the way toward its asymptotic value. Is that a reasonable estimate of the time to wait before 95% of the full effects of CO2 accumulation to date have occurred?
SM, you mean fig.2 in this paper?
http://pubs.giss.nasa.gov/docs/2010/2010_Lacis_etal.pdf
Zero out all non-condensing greenhouse gases–that includes CO2.
“Model initial conditions are for a preindustrial atmosphere.”
That model doesn’t include any anthropogenic (accumulated) CO2.
I’m very skeptical about all of this. Fair enough more co2 leads to more temperature, and with more temperature you get more water vapor and so on..
But here is a simple question, if temperature is a key component, then:
What is the heat content of the upper ocean (700m)?
What is the heat content of the lower atmosphere (10km)?
Lets get some context…
The Lacis paper looks like it runs a model out to year 50, achieving a drop in temperature of some 35 C in that time, but this can’t really be an equilibrium response and the paper doesn’t go into the detail required to interrogate Septic’s question thoroughly.
Isaac Held recently gave a talk in Wisconsin on the topic of how one could usefully decompose the evolution of the surface response to global warming by a fast component (which is proportional to the radiative forcing) and a slower component which reflects the response of the deep ocean. Right now, the response to increasing CO2 has been dominated by the fast component, with relatively small influence from the slow component (but which grows in time). This also emphasizes the utility of the transient climate response for timescales relevant to the 21st century. In fact, the two timescale components have different spatial structures (e.g., less relative warming in the Southern Ocean at first, and a reduction in the land-ocean warming ratio over the slower timescales); it follows that the changing relative magnitude of these two components actually introduces time-dependence into the strength of the climate sensitivity.
What’s more, forcings, even short-lived ones, have remnants that lurk in the climate system on long timescales. Signatures of Tambora or Pinatubo for example are still existent in the deep ocean. The literature on volcanic responses has been pretty weird about making this clear though (see e.g., Stenchikov et al 2009)
elspi @28 — Post in haste, repent at liesure. (Referring to my prior two back-to-back comment). Regarding the infinite series, it only converges in the open interval (-1,+1) as you state. However, read on.
earlier, I didn’t write down quite the right equation. For response R with forward (open loop) gain g, feedback f and forcing F, in the s-plane one has
R = Fg/(1-gf)
If g=1 then the formula is, of course, just
R = F/(1-f)
Now this equation is readily solved for any rational functions F and f, but only has physical significance when the roots lie in the right hand portion of the s-plane, including the imaginary axis as a limiting case. Stated more simply, f is bounded above by +1. But the feedback can be as negative as may be. For example, if f = -1000 then R is approximately 0.001F. The simple infinite summation doesn’t apply for f less than or equal to -1 and of course one can check everything in the time domain using convolution, but viewing this small point in the s-plane is much the easier.
Apologies to all for not having been more careful the first time around.
http://www.physorg.com/news166196667.html
“… Until the new description of seawater is widely adopted, ocean models will continue to assume that the heat content of seawater is proportional to a particular temperature variable called ‘potential temperature’.
“The new description allows scientists to calculate the errors involved by using this approximation while also presenting a much more accurate measure of the heat content of seawater ….
“The difference is mostly less than 1 degree C at the sea surface, but it is important to correct for these biases in ocean models….”
[Response: This is an improvement in theory, but for it to be an improvement in practice needs all of the ocean codes to track carbonate and other ions as well as salt, which figure in the density equation. NB. the GISS-E-R model already uses enthalpy as the state variable and so had more-accurate-than-standard thermodynamics anyway. – gavin]
Isotopious @39 — I have been fiddling with a two resevoir (two box) model.
The first resevoir represents the atmosphere and that portion of the ocean, the upper few meters, which is at the “same” temperature as the bottom of the atmosphere just above it due to the mixing via wave action. Since I only have data with yearly averages available, I fix the time constant of the response of this resevoir to be one year.
The second resevoir represents the so-called mixed layer of the ocean, your nominally 700 meters. This resevoir has a characteristic time of 30 years as I am under the impression that is what happens in ModelE.
The parameter estimation program determines the sizes of these two resevoirs by best fit to GISTEMP using the annualized globalized total forcings from 1880 CE through 2003 CE available on the GISS website. The fit is quite impressive once a fraction of the SOI, with a 7 month lag, is subtracted from GISTEMP.
43
Yeah I have often heard a few meters of the surface ocean is equal to the entire atmosphere with respect to heat content, so the upper ocean (700m) has somewhere near a thousand times the heat content of the entire atmosphere (but I have no idea, this is a guess)… What I would like is a better estimation, since I have not been able to find it anywhere (I can only find anomalies which tell me nothing about the total).
Then of course we line up the heat content and compare them with each other.
.2 (co2) = .8 (water vapor and clouds) = 1 (atmosphere heat content)
= 1000 (ocean heat content).
This is not plausible.
40, Chris Colose
Thank you.
The literature on volcanic responses has been pretty weird about making this clear though
Pretty weird? As in, not making it clear at all?
to others, I was referring to this paper, referenced earlier in the thread: Andrew A. Lacis, Gavin A. Schmidt, David Rind, and Reto A. Ruedy, 2010: Atmospheric CO2: Principal Control Knob Governing Earth’s Temperature. Science 15 October 2010: 356-359.
In Figure 2 it looks like the temperature response to removal of greenhouse gases is 95% of the way to equilibrium after 20 years or so. I left the “after 2 years or so” out of my post that Chris Colose responded to. Sorry.
Nice article Chris.
Just a repeat of a trivial point I made earlier:
This thermodynamic law says that the saturation pressure increases nearly exponentially with temperature (1)
Agreed.
(39) IIRC the specific heat of the atmosphere per unit mass is roughly the same as for water. A layer of water roughly 10M thick contains about as much mass as the atmosphere, therefore the thermal inertia of a 700M layer of water is circa seventy times that of the atmosphere. Of course we don’t just heat up the water uniforming as in raising a block of water 700Mdeep uniformly by 1C, the surface responds much quicker than the deeper layers.
Re #17 and #19.
[Stefan-Boltzmann and Maxwell-Boltzmann]
I probably disagree with that statement. No time to check. Anyway it might be safer to regard them as different. From a modern standpoint, and on the theoretical side, Boltzmann never got as far as Planck’s law and SB is its integral.
Very impressive math, etc.
But we all know where this is going and how it will end. You don’t have to be Einstein.
Is anyone planning for what will happen in the final chapter? What’s the survival plan? Go north? Get into a fetal position?