 Many of you will have seen the obituaries (MIT, NYT) for Ed Lorenz, who died a short time ago. Lorenz is most famous scientifically for discovering the exquisite sensitivity to initial conditions (i.e. chaos) in a simple model of fluid convection, which serves as an archetype for the weather prediction problem. He is most famous outside science for the ‘The Butterfly Effect’ described in his 1972 paper “Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”. Lorenz’s contributions to both atmospheric science and the mathematics of dynamical systems were wide ranging and seminal. He also directly touched the lives of many of us here at RealClimate, and both his wisdom, and quiet personal charm will be sorely missed.
Many of you will have seen the obituaries (MIT, NYT) for Ed Lorenz, who died a short time ago. Lorenz is most famous scientifically for discovering the exquisite sensitivity to initial conditions (i.e. chaos) in a simple model of fluid convection, which serves as an archetype for the weather prediction problem. He is most famous outside science for the ‘The Butterfly Effect’ described in his 1972 paper “Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”. Lorenz’s contributions to both atmospheric science and the mathematics of dynamical systems were wide ranging and seminal. He also directly touched the lives of many of us here at RealClimate, and both his wisdom, and quiet personal charm will be sorely missed.
Ed Lorenz had a reputation of being shy and quiet, and this was indeed the impression he gave on first meeting. Indeed raypierre was interviewed by Ed at MIT in 1979 for his first faculty job — and remembers having to ask most of the questions as well as answer them. But he also remembers a lot of timely support from Ed that helped smooth over the somewhat rocky transition from basic turbulence theory to atmospheric science. The longer you were around Ed, the more you came to appreciate his warmth and sense of humor. He was an avid hiker, and many in the community (our own Mike Mann included) have recollections of time on the trail with him around the hills of Boulder and elsewhere.
Lorenz launched the modern era of the study of chaotic systems, which has profound implications both within and beyond atmospheric science. We’ll say more about that in a bit, but the monumental work on chaos should not leave Lorenz’s other contributions to atmospheric science completely in its shadow. For example, in a 1956 MIT technical report, Ed introduced the notion of “empirical orthogonal functions” to atmospheric science, and this technique now plays a central role in diagnostic studies of the atmosphere-ocean system. He also pioneered the study of angular momentum transport in the atmosphere, and of atmospheric energetics. Among other things, he introduced the important notion of “available potential energy,” which quantifies the fact that not all of the potential energy can be tapped by allowable rearrangements of the atmosphere. Later, he pioneered the concept of resonant triad instability of atmospheric waves, an idea that has repercussions for the sources of atmospheric low frequency variability. As if that weren’t enough Ed also introduced the concept of the “slow manifold” — a special subset of solutions to a nonlinear system which evolve more slowly than most solutions. The atmospheric equations support a lot of very quickly changing solutions, like sound waves and gravity waves, but on the whole what we think of as “weather” or “climate” involves more ponderous motions evolving on time scales of days to years. Ed’s work on this subject launched the study of how such slowly evolving solutions can exist, and how to initialize a numerical model so as to minimize the generation of the fast transients. This is now part and parcel of the whole apparatus of data assimilation and numerical weather forecasting.
Ed was not a user of general circulation models. His essential approach was to crystallize profound phenomena into very small sets of equations for how a handful of variables change with time. He left behind him a dozen or so such models, each of which would repay many lifetimes of study. He was indeed a master of “seeing the world in a grain of sand.” You can read about some of these models in the talk raypierre gave at the 1987 Lorenz ‘retirement’ symposium — not that this slowed him down!
Now let’s take a closer look at that butterfly effect. Despite the fact that there are no butterflies or tornadoes in climate models, Lorenz’s discoveries and their implications played a central role in climate modelling efforts and in the most recent IPCC report.
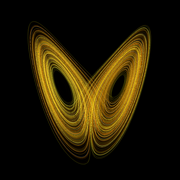
The mathematically inclined reader who takes a look at Ed’s early papers on what is now called the “Lorenz Attractor” will be astonished at the depth and modernity of his ideas about chaos. This line of work was no mere remark on a numerical exercise. Lorenz actually teased out the geometry of chaos — the many-leaved structure of the attractor — realizing that it was no simple geometric entity like a sphere or a folded sheet of paper. It was indeed “strange” in a sense which he made geometrically precise. This is why the work had such lasting impact on the area of pure mathematics known as dynamical systems theory. He went beyond that to develop or apply many fundamental concepts in chaotic systems, quantitatively formulating various measures of predictability and connecting the Lyapunov exponent — a certain precise mathematical characterization of chaos — with the structure of strange attractors. But that’s for the mathematicians. What makes Lorenz’s work interesting to the entity on the Clapham omnibus is the notion of sensitive dependence on initial conditions. Some have even seen in this deterministic chaos the resolution to the problem of free will!
The idea that small causes can have large and disproportionate effects is not at all new of course. The poem: “For the want of a nail, the battle was lost” (medieval in origin) encapsulates that well, and popular culture is full of such examples, “It’s a wonderful life” (1946) and Ray Bradbury’s “A Sound of Thunder” (1952) for instance. Curiously, Bradbury’s story also involves a butterfly, and since it predates Lorenz’s coining of the phrase by a decade or so, people have speculated that there was a connection to Lorenz’s choice of metaphor (he started off with a seagull in his 1963 Trans. N.Y. Ac. Sci. paper). But that doesn’t appear to be the case (see here for a history). It’s worth adding that all of Lorenz’s papers were exceptional in their clarity and are well worth tracking down as an example of science writing at its best.
However, the difference between the long-standing popular conception and Lorenz’s work is that he demonstrated this effect in a completely deterministic system with no random component. That is, even in a perfect model situation, useful predictability can be strongly limited. Strictly speaking, Poincaré first described this effect in the classic three-body problem in the early 1900s, but it was only with the onset of electronic computers, as used by Lorenz, that this became more widely recognised. To throw in another popular culture reference, Tom Stoppard’s Arcadia has a character, Septimus, who drives himself mad trying to calculate chaotic solutions to the logistic map by hand.
So what does this have to do with the IPCC?
Even though the model used by Lorenz was very simple (just three variables and three equations), the same sensitivity to initial conditions is seen in all weather and climate models and is a ubiquitous phenomenon in many complex non-linear flows. It is therefore usually assumed that the real atmosphere also has this property. However, as Lorenz himself acknowledged in 1972, this is not directly provable (and indeed, at least one meteorologist doesn’t think it does even though most everyone else does). Its existence in climate models is nonetheless easily demonstratable.
But how can climate be predictable if weather is chaotic? The trick lies in the statistics. In those same models that demonstrate the extreme sensitivity to initial conditions, it turns out that the long term means and other moments are stable. This is equivalent to the ‘butterfly’ pattern seen in the figure above being statistically independent of how you started the calculation. The lobes and their relative position don’t change if you run the model long enough. Climate change then is equivalent seeing how the structure changes, while not being too concerned about the specific trajectory you are on.
Another way of saying it is that for the climate problem, the weather (or the individual trajectory) is the noise. If you are trying to find the common signal that is a signature of a particular forcing then averaging over a number of simulations with different weather works rather well. (There is a long standing quote in science – “one person’s noise is another person’s signal” which is certainly apropos here. Climate modellers don’t average over ensemble members because they think that weather isn’t important, they do it because it gives robust estimates of the signal they are usually looking for.)
The ensemble approach, and indeed the multi-model ensemble approach, used in IPCC then derives directly from Lorenz’s insights into his serendipitous numerical problem.
Note the effect of the Butterfly Ballot and a few hanging chad.
Please see http://climatesci.org/2008/04/23/comment-on-real-climates-post-on-the-relevance-of-the-sensitivity-of-initial-conditions-in-the-ipcc-models/
[Response: In the linked piece, you very clearly state that you do not believe that the real world is sensitive to initial condition variations like butterflies. That is all we are discussing here. If you now think that it is, feel free to expound on your viewpoint. We were just trying to make sure that a diversity of points was presented. – gavin]
Ed Lorenz was one of the great figures of 20th century science, and he was an accomplished writer as well. His book, “The Essence of Chaos” is still the best popular science book on the subject. It is loaded with interesting commentary as well:
Ed Lorenz then goes on to provide the clearest and most concise description of the ocean-atmosphere system I’ve ever heard:
He then goes into a really great description of the predictable and the irregular (after a brief discussion of how strong winds can produce anomalously high tides):
Thus, we can think of efforts at climate prediction as being focused on the regular components of the land-ocean-atmosphere system. As a simple example, think of dropping a china cup on a tile floor from a two meter height. One can quickly predict the velocity of the cup at impact as well as the time the cup will hit – but try predicting the number of pieces the cup shatters into, and where those pieces all end up. (The notions that Lorenz came up with had such far-reaching effects in mathematics that people like Ian Stewart claimed him as one of their own, as well).
Unfortunately, a number of widely-quoted commentators on global warming seem to have little understanding of this entire issue. For an example of a heavily distorting “science article”, see the LA times:
http://www.latimes.com/news/science/environment/la-sci-adapt26mar26,1,3720995,full.story
“Global warming: Just deal with it, some scientists say: The ‘non-skeptic heretic club’ says it would be easier and cheaper to adapt than fight climate change. Critics say the flaw in the theory is that the effects will be unpredictable. “(March 26 2008)
No – the flaw in the theory is that the climate effects ARE predictable – that’s the regular component! There is high uncertainty about the upper bound of responses, is all. What is remarkable is that the press is giving so much coverage to such a notion – well, maybe not, after what we’ve seen so far.
For another example of this fundamental lack of understanding, see:
http://sciencepolicy.colorado.edu/admin/publication_files/resource-2593-2008.08.pdf
This is the latest last-ditch effort to prevent governments from taking action on global warming. Essentially, there is a small group that is trying to convince the world that doing nothing about global warming is the right thing to do.
However, those authors – Pielke, Green and Wigley – have no idea of what they are talking about. None of them has any background in energy technology whatsoever, yet they feel they have some authority – and apparently Nature agreed. None has ever published any papers on actual energy technology – solar PV, for example – and yet their paper – an attempt at predicting future technology scenarios – was accepted and published by Nature.
The fact of the matter is that existing energy technology is sufficient to replace all fossil fuels – it is just a manufacturing and infrastructure issue. Thus, Pielke et. al’s analysis is completely bogus. I can’t imagine why Nature would allow people with zero research experience in solar, wind, biogas, other biofuels, or nuclear to write such an article. What specific “enormous advances in technology” are needed? I doubt that the authors could even write down a theoretical description of a PV cell without a lot of help.
A far more interesting question, though, is what the regular and irregular components of attempts to forecast energy development are. We know that enough sunlight falls on the Earth in one hour to power all of human society for one year – so we just have to capture and convert a small fraction of that in order to meet our energy needs. That is the regular component.
Thank you for this obit. Lorenz does indeed deserve to be praised more than buried. Your comments about chaos theory are particularly germane given the common misconceptions about chaos in climate and climate models. Lorenz’s story illustrates how scientists can become intrigued by a problem and can’t put it down until they not only understand it, but can explain it clearly to their peers.
WRT how climate can be deterministic even as weather is chaotic, it helps me to think in terms of conserved quantities and the regions they constrain a system to in phase space. A system may have many states it can occupy within that constrained space, but the long-term averages over those states will not vary much even given small perturbations.
It is a shame that we have lost someone who was so adept at communicating complex ideas with such lucidity, brevity and precision at the same time. I mean no offense to the authors of this site when I say that I feel that Lorenz was unmatched in this regard. His skill with words is something that I — and many others — aspire to.
[Response: Believe me, no offense could possibly be taken. It’s an honor to be even put in the same sentence as an expositor such as Ed. Most of us would be happy to achieve a half the clarity of what he did in his writing. –raypierre]
I was looking through his publication list, and he published 4 papers in 2006! Remarkable.
For those readers who are not climate scientists or mathematicians, I can recommend James Gleick’s 1987 book Chaos: Making a New Science which does a very nice job of telling the story of how Lorenz made his serendipitous discovery and explaning the basic ideas and implications of choas theory for climatology and other fields. A good read.
Re: #3,
Another, at least to me, interesting question is just what exactly are our so called needs? As an example of what I mean let me postulate a possibly radical paradigm shift and alternative way of life. Do we really need what we think we do? Could we imagine a much more personal self contained but still comfortable and fulfilling existence? We living in the so called first world style of Western civilization live in relatively large houses with lots of power consuming lights and gadgets. Do we really need to light an entire room to full daylight standards at night all the time? could we survive with low intensity LED strips and maybe wear self contained fashionable headgear with personal high powered lighting powered by human powered kinetic generators. Maybe saving the full daylight at night brilliance for very special occasions? I can think of hundreds more such examples of energy efficiency which is available right now with off the shelf technology if we look at how and what we do from radically different perspectives. I’m not even going to bother with pointing out the stupidity of sitting in a typical traffic jam commute to your average downtown office, cocooned in a couple of thousand pounds of fossil fuel powered carbon dioxide spewing automobile. As a more concrete example one of my colleagues from work takes three to four days of very stressful travel by plane, rental car hotel stay etc… to visit and implement my company’s software on site at a typical customer. In that same time I can log on to computers in half a dozen countries around the world and do the same implementation and training for dozens on customers with ever leaving my home. Maybe I can invite those customers to meet me on some nice sunny beach on our two month long sabaticals and make it a point of all of us getting there by sailboat instead of by plane. Let me invite all of you to start imagining this kind of world. BTW I just came back from doing kayak support for a relay swim team http://www.distancematters.com held in Tampa Bay Florida in commemoration of Earth Day, I spent over 13 non stop hours paddling in this 24 mile race. I met some people who do things like swim the English Channel run up on the beach turn around and then swim back again, It was an immense honor and a pleasure to be associated with such people.
Happy Earth day to all!
Thanks for a very nice scientific obituary. In addition to his writing, Lorenz’s oral presentations were also marvels of astonishing clarity. I always was left at the end of his talks with the distinct impression that his brain neurons were deterministic while mine were chaotic.
[Response: no distinction then? – gavin]
A fine scientist, a fine man, and a fine human being. I will mourn him.
Re #3, on energy security and replacement of fossil fuels. I am unsure as to the notion of the technology being available presently to replace fossil fuel enough to mitigate climate change. The big issue over here in the UK at the present time is Energy Poverty. Fossil fuels are cheap, renewables are more expensive and hence that will drive fuel bills up. If we produce 20% of our energy from sustainable/renewable sources then energy is presently going to cost more putting millions of homes into energy poverty which is defined as 10% of income being spent on energy expenditure.
In the UK petrol (gasoline) is on the rise, £1.10 a liter and diesel £1.20 (that equates to almost $7 a US gallon), gas and electricity prices have risen significantly in the past two years and although this makes renewables more affordable as fossil fuels become more expensive more R&D is required before this price difference is closed. Our Government or anyone else for that matter has not mentioned this to the people. I wonder why.
Edward Lorentz – RIP. I knew of him through my laymans studies if fractals, chaos and nonlinear dyanamics. James Gleiks Book CHAOS mentioned him a lot. He seemed a very capable and judging by this article brilliant scientist.
I read the little companion piece by Richard Eykholt, and I think a point is being missed. It is not that the flap of the butterfly wings in Tokyo is “causing” the tornado, in so far as creating the kinetic and thermal energy differentials that result in a tornado. Rather the flap of the butterfly wings can set up an escalating sequence of variations in the temporal and spatial pattern of energy flows (as compared with the non-butterfly case), that ultimately could result in the tornado happening in June in Dallas, rather than in May in Oklahoma City. It is somewhat analagous to a pinball machine. A very very minor change in the initial velocity vector of the ball results after a period of time in a completely different, even unrecognizable, path for the ball. A brief nudge on the table is not construed to set the ball in motionr, nor is it construed to create the energy exchange between the ball and each bumper it contacts. Rather, a very minor initial change to the ball’s path results after time in a totally different pattern for the ball’s motion. Threshold phenomena, just like barely missing a specific bumper, become significant markers in the pattern change.
One thing I’ve wondered about. Ed’s writings were always so clear that they came across as just about the only way to express a scientific idea in writing. They expressed the idea effortlessly. In my experience, such effortless communication is anything but effortless. For those who worked with him, could you describe his approach to problem solving and subsequent communication of the results. Was he intuitive–like Landau for example–or did he need concrete examples he could study and draw insight from? And did he write his papers in a single draft or did they undergo many revisions? Thanks.
Gavin – Thank you for posting my Climate Science link. It terms of actual butterlies, as clearly explained by an expert in the physics and mathematics of nonlinear dynamics and chaos in geophysical flows, Professor
Richard Eykholt (see http://climatesci.org/2005/10/12/more-on-the-butterfly-effect/), where he writes
“Roger:
I think that you captured the key features and misconceptions pretty well. The butterfly effect refers to the exponential growth of any small perturbation. However, this exponential growth continues only so long as the disturbance remains very small compared to the size of the attractor. It then folds back onto the attractor. Unfortunately, most people miss this latter part and think that the small perturbation continues to grow until it is huge and has some large effect. The point of the effect is that it prevents us from making very detailed predictions at very small scales, but it does not have a significant effect at larger scales.
Richard Eykholt”
[Response: You misinterpreted this back on the original thread and you are misinterpreting it here again. However, just repeating the same argument is pointless. Since I agree with Dr. Eykholt’s statement, and so do you, let’s just leave it at that. (if other readers are interested in what this is about, please go to the original thread. The clue is that ‘larger scales’ in the Eykholt quote means the attractor itself (i.e. climate), while RP thinks he means the large scale flow (i.e. the specific position on the attractor)). – gavin]
pete best wrote: “Fossil fuels are cheap, renewables are more expensive and hence that will drive fuel bills up.”
The cost of fossil fuels is going up rapidly and will continue to do so, and in the not too distant future fossil fuels will be in increasingly short supply at any price due to depletion of supplies, and declining extraction rates. So fuel bills are going to be driven up in any case. Meanwhile the cost of clean renewable energy from wind and solar is dropping, and as both industries are growing rapidly worldwide, economies of scale combined with new technologies are set to reduce prices even more, perhaps dramatically so. There is every economic reason in the world to accelerate the phaseout of fossil fuels and the expansion of clean renewable energy sources (and of course for maximum efficiency in the usage of both).
[Response: Please, this is not at all an appropriate place to be discussing fossil fuel economics. –raypierre]
There’s some pretty libelous things said in this Esterbrook interview by that opponent of mine. Doesn’t take long to find them either. Downright shameful. Somebody should hand them their hat.
http://icecap.us/images/uploads/DonEasterbrookInterviewTranscript.pdf
[Response: Yes it’s pretty awful, but it doesn’t have anything to do with Lorenz. Can we please try to show a little respect for the topic? –raypierre]
Gavin- I agree readers can go through the thread to see the discussion. However, you are misrepresenting my views. Rich Eykholt and I are in 100% agreement on this subject. The question that was being discussed is whether an atmospheric perturbation as small as a real world butterfly could actually effect large scale weather features thousands of kilometers away. The answer, as given by Professor Ekykholt is NO under any circumstance. The perturbation has to be much larger (Issac Held, as I recall said meters in his NPR interview; I suspect it is a few kilometers or more) for a pertubation to effect an atmospheric feature thousands of kilometers away.
This issue, based on our disagreement, would benefit from further quantitative evaluation with both analytic and numerical models. We do have papers on the use of analytic models to examine chaos and nonlinear dynamics which document that we are quite familiar with the subject of sensitivity of the climate system to initial conditions; e.g. see
Pielke, R.A. and X. Zeng, 1994: Long-term variability of climate. J. Atmos. Sci., 51, 155-159.
http://climatesci.colorado.edu/publications/pdf/R-120.pdf
[Response: As we said above, this is what you believe. Why you accused us of misrepresenting you is a mystery. However, your claim about Ekykholt’s belief is contradicted by his quote above. He states very specifically that exponential growth saturates at the time the perturbation reaches the size of the attractor. That, for the atmosphere, is very large indeed and is certainly large scale enough to encompass storms thousands of miles away. Isaac can certainly speak for himself, but as far as I know there is no demonstration that there is a minimum scale below which perturbations do not grow. Such a thing may exist, but your certainty on the matter seems a little overconfident. Perhaps you’d care to point out a reference on the subject? – gavin]
RE #11 & 15, and if they stop all the tax-breaks and subsidies to oil that would jack up the price of oil (but save us some money come April 15th).
However, no butterfly flap will ever get those Hummer guys to switch to a Prius. You need a mamouth elephant stomping on and squashing all the Hummers to accomplish that, and even then it seems doubtful.
Our Univ is trying to get more into supercomputers — the hard sciences and computer sciences already are into them to some extent, but we may be getting access to an even more powerful supercomputer.
I’m just wondering what the social sciences can do with it. I’m not aware of any modelling formula that includes the true forcing of this bout of global warming — people and the psychological, social, and cultural dimensions of our human condition. These are not only highly complex, but in a reflexive feedback with “reality” as perceived through people’s (changing) sociocultural-psychological lenses.
I realize the various climate scenarios (for different levels of our human emissions) are meant to capture this behavioral science dimension. But it would be great if we could narrow down those scenarios.
And then there are relatively abrupt changes or somewhat discontinuous functions that are possible, for instance, revitalization movements (social movements in sociology), in which people change really fast. I’m just hoping for that — change in the right direction of reducing GHG emissions, due to a new vision for a better society and world.
I am sorry, but everything in the citation of Prof. Eykholt seems either inaccurate or backwards.
First, not every small perturbation on a strange attractor grows. Chaotic attractors usually have so-called hyperbolic local structure of the phase flow at almost any point, meaning that the vicinity of every trajectory has two manifolds, one expanding (led by Lyapunov exponent), and the other CONTRACTING, to maintain phase volume or have it shrinking for dissipative systems. Therefore, if the flap energy projects entirely on the contracting side of phase flow, this perturbation would decay, exponentially.
Second, if the perturbation did grow up to the attractor boundary and folds back, it is exactly where unpredictability occurs; it is unpredictable where the system state would land on the next turn. The butterfly “effect” is not that it would trigger growing contiguous squalls of tornados in Texas, but it would affect the time or place _when/where_ a tornado would strike. Tornados in Texas will occur no matter what, but their time and place could be traced back to a butterfly flap in Brazil, hypothetically speaking.
Third, it is exactly opposite of what was said about detailed predictability on small scales: locally, the phase flow on attractors is pretty simple almost everywhere, and therefore is easily predictable. Anyone can predict their weather along a trajectory of 30 seconds long.
About “effect at large scales”, it looks like the original question was misunderstood. About the actual relationship between a butterfly flap and large scale effects, see my explanation here:
http://climatesci.org/2007/05/18/wg1-ipcc-chapter-1-more-scientifically-erroneous-statements/#comment-179850
Cheers to global climatology,
– Alexi Tekhasski
Re #17: In the interview with NPR, I was caught off guard when asked if a butterfly was big enough — I was thinking that the scale of the perturbation has to be larger than what is often referred to as the Kolmogorov microscale, the scale below which the flow is effectively laminar, to avoid being damped out immediately. This scale is typically a few millimeters in the atmosphere — so its an academic point even if true, which, in retrospect, is not self-evident. Not being able to articulate any of this during the interview, I just blurted out “a meter” as the scale require, while trying to visualize if the flap of a butterfly’s wings was turbulent. Afterwards I regretted questioning Ed’s choice of perturbation. I don’t think there is any question that once one perturbs turbulent scales the perturbation will grow to affect the entire atmosphere.
The unpredictability of weather doesn’t matter to climate predictions,
but the proper modeling of weather does. The tornado in June in
Dallas might have the same effect on climate as the tornado in May in
Oklahoma City, but how about 100 tornadoes versus zero? It’s easy to
think that weather averages out, hence the example of one tornado
versus a different one. But weather does not average out, weather is
climate. The diurnal cumulus the past few days here in No. VA due to
the recent rains are affecting the climate and are not averaged out by
the lack of clouds somewhere else.
More to the point, the effect of some butterfly somewhere on this
weekend’s upper low and Monday’s rains will have it’s corresponding
effect on the rest of next week’s climate in our area. It matters in
the short and medium range whether the upper low moves out to sea or
travels down to North Carolina like last Sunday’s upper low. Having
these lows two weeks in a row will have even more effect on our future
weather and thus climate. Weather forecasters don’t use expressions
like “when in drought, leave it out” for continuity only. It often
does not rain in a drought because of the local lack of moisture, not
the broader weather pattern. Today’s butterfly and this coming
Monday’s upper low may indeed prevent some drought next month. Our
weather can affect our climate.
There are workarounds for correcting weather in climate models, such
as doing detailed weather modeling for a small representative area
using parameters from the climate model, then applying the resultant
parameters from the weather model back into the climate model. Or
using real world weather measurements for the parameters in climate
model . But the first workaround doesn’t fully address the
idiosyncrasies of terrain, land and ocean that affect the weather
(such as the Appalachian mountains here). The second workaround
doesn’t fully address the effect of climate changes on real world
weather (i.e. current weather measurements may not apply in future
climates). Still those workarounds are better than nothing and
getting better all the time. And weather modeling in climate models,
particularly the spatial and temporal resolution, will ultimately make
my whole point moot (within 20 years at most).
I think was a leader in scientific thought in so many ways, not the least was his understanding that everything is related and interrelated to everything else in the universe and nothing is superfulous. Hense the more scientists know the more (the smart ones that is) they realise the enormity of what they dont know. For every item of knowledge they understand there forms an squaring of the items they do not understand…yet.
Just seen that CO2 production was at a record high last year and that now atmospheric CO2 concentration is up to 385ppm –0.6% up than from 2006. Methane was up as well for the first time in ten years..to early to tell if that was just a glitch or readjustment or that the melting of the tundra may have contributed.
Eric,
Realclimate has addressed the issues of regional climate several times before. Indeed, this is an area where more work is needed, especially if you want to assess/bound the costs of climate change. Modeling global climate is more forgiving, and it can also give you important information that helps you in making regional assessments. An open system (e.g. regional climate) will always exhibit more seemingly chaotic behavior than a closed one (global climate).
Say more about Lorenz, please. This thread is about him and his work.
This is an excerpt from Appendix 1, Essence of Chaos, Ed Lorenz:
Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas?
Supercooled water, when tapped slightly, gives a vivid example of one kind of possible effect. If the water is allowed to slowly warm up to the freezing point, nothing happens. If jiggled, or if even a single ice crystal is added, however: http://www.youtube.com/watch?v=DpiUZI_3o8s
So it is not just the perturbation, it is the state of the system at the time of perturbation. Jiggling water at 50C will not cause it to flash into steam, for example.
A more relevant weather example is that of a “conditionally unstable parcel of air” – as explained well at wiki:
In this case, the amount of water vapor in the air will determine the sensitivity of the “air parcel” to perturbations – and “sensitive dependence on initial conditions implies chaos” – but chaos does not imply a total lack of predictivity.
So, what sets the boundary conditions for weather systems? Can we look at climate prediction as an attempt to forecast those boundary conditions? One main boundary condition is sea surface temperatures – leading to this 1998 paper:
http://ptolemy.gmu.edu/~beall/data/chaos_papers/shukla-1998-science-v282.pdf
The paper has a discussion of limitations to predicting the frequency and intensity of El Nino events, but the point is that the ocean plays a major role in setting boundary conditions for weather systems. This is not some new realization – it’s been know for quite a while, despite efforts by some to present this as their new, sole discovery:
http://www.jsg.utexas.edu/news/feats/2007/pielke.html
Usually, when people make such large mistakes they print retractions.
Ray, I agree with your last two sentences, except that my impression is that global climate is the average of regional climates. Although that smooths out the chaos of the regional climates, it doesn’t avoid their complexity. The fact that the global climate is a closed system doesn’t really help since it can’t just be simply modeled with energy equations. The complexity of the regional climates must be modeled to determine the effects of clouds in particular and all forms of water in general. Those can then be averaged or used as parameters in a global climate model.
Eric, I’m afraid I agree with Hank–we should be celebrating Lorenz here. Just want to say that you don’t have to get things 100% right on a regional scale to have a good enough global climate model. The more closed the system, the closer it comes to having its state space determined by conserved quantities. Earth comes pretty darned close.
[Response: I certainly don’t think Ed would have had any objection to lively, even contentious, discussion of the nature of chaos, or its implications. We don’t have to stick to encomium, but I was making a plea to try to at least keep the discussion from just becoming a dumping ground for disconnected random thoughts of the day. –raypierre]
In the spirit of this memorial to Lorenz and the seminal discovery of “deterministic non-periodic flow”, it is of interest to recall a little more of Barry Saltzman’s role, as I heard him tell it around 1990. Barry is now deceased.
With regard to:
“Lorenz found this (chaotic) phenomenon by accident …and
… it was only with the onset of electronic computers, as used by Lorenz, that this became more widely recognized.”
Barry himself did the first numerical integration of the 3 non-linear equations and so was the first person to witness/discover the chaotic behavior. He then showed the results to Lorenz, showing that the solution was “non-repeating” — contrary to their expectations at the time for relatively simple, albeit non-linear, coupled ordinary differential equations.
Barry, always the gentleman, nevertheless was completely reverential to Lorenz about the discovery saying “… he (Barry) could never have written… “ the analysis presented in the original 1963 paper.
[Response: Indeed, this is a very fair description of the sequence of events, both with regard to Saltzman’s important role in the discovery and Lorenz’s seminal contribution to the analysis. By the way, what got Lorenz interested in this sort of equation originally was a desire to demonstrate the deficiencies of statistical methods of weather forecasting, as opposed to dynamically based forecasts. –raypierre]
Gavin – I am glad this discussion is continuing. I will be having more to say on this next week in a weblog on Climate Science, however, you are failing to distinguish between an open and closed system, and between the real world and models.
With nonlinear atmospheric models such as analyzed by Professor Lorenz, the results for large scale features are sensitive to the initial conditions regardless of how small they are. This is because the system is closed.
The real world climate system, however, is not closed, such that energy (i.e. in the form of heat) can leak out of the system. In the case of such a small perturbation as the flap of a butterfly wing, the kinetic energy of the small amount of turbulent air that it generates will quickly dissipate into heat, once the flapping stops. Radiative loss of this heat to space will prevent the flapping to have any effect at large distances.
This is one of the reasons that you are mistaken in stating that “there is no demonstration that there is a minimum scale below which perturbations do not grow.” If a perturbation in the system (i.e. the atmosphere) dissipates into heat, it can be lost to the system before affecting atmospheric features at large distances. I will have more on this topic on my weblog next week, and will post a comment on Real Climate when it appears.
[Response: Have a look at Isaac’s remark above. I think what you probably have in mind is the possibility that if a perturbation is at a scale where you have primarily downscale energy cascade to the dissipation range, it might never project on the large scale quantities whose behavior determines large scale predictability loss. Given the nature of turbulence, it is hard to absolutely exclude this possibility a priori, but for this to happen, there would have to be ZERO leakage to large scales. Not just small but ZERO. That is exceedingly unlikely, and would be contrary to most of what is know about turbulent cascades. As a practical matter, I do agree that if the initial perturbation is at sufficiently small scales, the projection on large scales would be small enough that it could take an exceedingly long time before it affected the evolution of the large scales. –raypierre]
Re: 29
As far as I remember, Lorenz considered an open system in his original paper – there was a heat source.
I don’t think it matters whether the system is open or closed. What is more important, I believe, is the multiplicity of characteristic spatial scales. In the Lorenz system there are only two: the global scale and the dissipative scale. This is why butterfly affects solution everywhere. In real atmosphere there are multiple spatial
scale, including local convective and synoptic. The butterfly perturbation could be dissipated within the containing spatial scale so that larger scales will never feel the effects of the butterfly wings flap.
I’m going to botch this story but I’ll tell it anyway. As many of you know Steve Smale was sort of the grandfather of modern dynamical systems theory. He created the “horseshoe map” which abstracts the necessary mathematical ingredients for a strange attractor down to squishing, stretching, folding the square.
Jim Yorke told me this next which is sort of amusing. Yorke is a brilliant dynamicist in his own right coined the word “chaos” for chaotic dynamics in his paper “Period 3 Implies Chaos”. It was bout 10 years ago so I’m probably mucking it up a bit. Anyway, at some point York xeroxed his copy of Lorenz’ famous paper on chaos “Deterministic Nonperiodic Flow” which had his name on the front and mailed it to Smale. This led to terms around around Berkeley such as “York’s discovery of Lorenz”.
RayPierre nailed this whole silly argument in his response to #29.
I do wish that Roger Pielke Sr. would present some concrete examples of his claim that sensitive dependence on initial conditions depends on whether the system is open or closed.
Take the example of a conditionally unstable parcel of air that has just reached the saturation point with respect to water vapor – a flap of a butterfly’s wings then could be the minor perturbation that sets off turbulent mixing. The timing of events is then really what is subject to the butterfly effect – not the final thermodynamics.
Take another example – models of hurricanes. See http://scitation.aip.org/journals/doc/PHTOAD-ft/vol_59/iss_8/74_1.shtml for Kerry Emanuel’s article, Tempest in A Greenhouse, in Physics Today:
Again, here we have a system poised at just the moment that some atmospheric perturbation – maybe a butterfly flapping its wings, or someone waving hello – initiates as sequence of events that can end in a category 5 hurricane – but only if a number of conditions (one being adequate SSTs) are met. The timing of events is chaotic, and the system is open – not closed.
To quote Lorenz again:
Thus, chaos isn’t the ultimate cause of the hurricane, just the proximate cause. I think Roger Pielke Sr. also is misunderstanding the statement, “there is no demonstration that there is a minimum scale below which perturbations do not grow.” Take for example the source of the eastern African waves that “seed” hurricane systems: http://www.aoml.noaa.gov/hrd/tcfaq/A4.html
There is no connection between the number of African easterly waves and the number of hurricanes, but they still set the timing of hurricane systems – even though only some fraction develop into hurricanes. Can the flapping of a butterfly’s wings affect the timing of the formation of an easterly African wave? If so, then the Pielke argument is somewhat mistaken.
If we rephrase it as this: “there is no demonstration that there is a minimum scale below which perturbations do not cancel each other out”, we can ask “can the flapping of one butterfly’s wings cancel out the effect of the flapping of another butterfly’s wings?” – and so on.
Let’s also look at the oceans – what about the timing of El Ninos? Are there perturbations in the net state of the tropical Pacific Ocean-Atmosphere that can lead to the formation of an El Nino when the system is poised to produce an El Nino? El Nino forecasts are successful on the scale of months, not days or weeks – so there the ocean is playing the leading role.
How about much longer timescales? On such timescales, a major volcanic eruption is just a small perturbation. Can it have a large effect? Imagine the world at the beginning of the Last Glacial Maximum, but not without full glaciation yet. Could a large volcanic eruption like Pinatubo then cool the climate enough to really lock in the ice age? Probably. Such a volcanic eruption would not have the same long-term effect if it happened 8000 years ago.
The thing to remember seems to be that all chaotic systems have different degrees of predictability, which always depends on the details of the system in question and the timescale of interest, and which also evolve with the system (i.e. with changing boundary conditions). One can easily imagine situations in which the weather is even less predictable than it is now – on a waterless world, for example, with no stabilizing ocean surface.
Ray – Thank you for getting involved in this discussion. The question of the leakage time scale is, of course needed, in order to determine when the exceedingly long time scale becomes infinite (in terms of where the heat goes). If we both agree that ALL of the turbulence quickly dissipates into heat when the flapping stops, then what is your estimate of the residence time of this heat within the atmosphere before it is lost to space?
Also, as another thought example, if a butterfly flaps its wings inside a room with the doors shut, would you still maintain that this has an influence on atmospheric circulation at large distances? All of the heat generated would be absorbed by the walls of the room, and subsequent heat conduction is, of course, laminar. An analogous behavior will occur in a very stable boundary layer (and any region of the atmosphere for such small perturbations), and if we can agree on this “exception” than we have made progress in understanding this issue. My point here is that if there is an part of the process which results in complete loss of the turbulent flow, then it is not communicated over large distances.
Issac’s Held’s answer also actually contains part of the answer on this issue. If the turbulence dissipates into heat, as illustrated in the above example, than its further behavior can be described by non-turbulent behavior. As he explained, he was “was thinking that the scale of the perturbation has to be larger than what is often referred to as the Kolmogorov microscale, the scale below which the flow is effectively laminar, to avoid being damped out immediately. This scale is typically a few millimeters in the atmosphere “. This is what occurs with the flapping of the wings of a butterfly; all of its energy dissipates into heat and the spatial structure of this heated air is less than a few mm. To disprove this total transfer downscale, one would have to show that a coherent turbulent structure remains and becomes progressively larger in scale and/or is monitored propagating away from the location of the flapping wings as a coherent disturbance of the air flow; in both cases, while still retaining the conservation of total energy. Since the total energy of the flaps of the butterfly’s wings must be accounted for (as kinetic energy in the turbulence, heat) what is your estimate of the magnitude of this energy that reaches thousands of kilometers away, as well as the path this energy would take to get there?
[Response: Regarding the butterfly in the room — even in a jar in the room — sure I think it’s likely that it would ultimately affect the large scale weather. Look at it this way: Temperature has a dynamic influence through buoyancy. The heat dissipated by the butterfly might warm the room by a few tens of microkelvins, say. That increased temperature will change the heat flow between the house and the environment, which will ultimately change the temperature of some parcel of air by a few nanokelvins. Then before you know it, some parcel of air the size of the state of Illinois has a temperature different by maybe a few picokelvins. I guarantee that if you take a GCM and change the temperature of the air over Illinois by a few picokelvins (given sufficient arithmetic precision) that that will lead to divergence of the large scale forecast given infinite time. I have seen no indication either in dynamical systems theorems or in numerical experiment to suggest that anything else would be the case. –raypierre]
I agree that if the atmosphere behaves as a Lorenzian system then Ray’s comment above is right and I can’t think of a reason why not. If so, however, the possible future states of the atmosphere must be a very large number just considering the numbers of butterflies and other atmospheric perturbators of various sizes, locations and times.
neutrino
Ray,
Doesn’t the “butterfly effect” imply a very large number of possible future atmospheric states given the vary large number of atmospheric perturbators?
neutrino
[Response: It’s better to think of it as uncertainty in knowledge of the future, rather than trying to decide what is meant precisely by a phrase like “possible future atmospheric states.” At any given time, you are lacking knowledge of what the various perturbators are going to do, and also lacking knowledge of the precise initial condition. This leads to a bundle of different trajectories the atmospheric state can evolve through, which will come to occupy a certain volume in phase space. Now, where climate vs weather comes in is that, if you are increasing CO2 at the same time, while those uncertain futures are splattered all across phase space, the at year 2100 splatter will nonetheless be confined to a region of phase space where, say, the global mean temperature is between 3.5C and 4C warmer than the present. In thinking about uncertainty about possible future states, you also need to distinguish between uncertainty due to “weather noise” of that sort, uncertainty due to possible different representations of physical processes (what will clouds really do? How fast will Greenland melt? Will land ecosystems start becoming a net carbon source?), and finally uncertainty in the future rate of emissions of CO2 by human industrial activity. –raypierre]
Ray- We certainly disagree with respect to the butterfly in the room in a jar. :-). Other readers of Real Climate (and Climate Science) can make up their own minds on this.
You are, however, taking the concept of chaos too narrowly and are focusing on idealizations (simple illustrative models and GCMs) of how the real atmosphere (and climate system) works. You are ignoring the consequences of the dissipation of kinetic energy into heat within a open system. The “picokelvins” of heat, even if they could cause such a temperature perturbation over the state of Illinois (which it would not), would be lost to space long before an “infinite” time were reached.
[Response: Roger, I can’t make sense of what you’re trying to say here. For those picokelvins of temperature to be lost to space, first they have to appear in the atmosphere as an increase of temperature, right? So there you have your change of one digit in the initial conditions, just like in Lorenz’s example. And your statement is just flatly inconsistent with thermodynamics. The butterfly dissipates heat locally, and that heat will be gradually diluted over a larger and large area. So just divide by Cp and there’s your answer. Do you think there’s some way to magically teleport the heat away, leaving the fluid to heal back to exactly the same condition it would have had without the flap? That’s really a stretch. Your remarks about simple models and GCM’s don’t make much sense to me either. The GCM doesn’t resolve butterfly-scale motions, but once you have influenced a dynamic variable (e.g. temperature) at a resolved scale, any number of actual twin experiments in GCM’s confirm the divergence. If you are claiming there’s some fundamental difference between sensitive dependence to large scale changes in a GCM and sensitive dependence in the atmosphere, I’d like to see some evidence to back up that claim. The success of GCM’s in short term weather forecasting would be pretty much impossible to reconcile with such a claim. –raypierre]
Roger Pielke Sr. says:
This is missing the point entirely. Again, let’s look at a specific example: the generation of Easterly African Waves.
R.W. Burpee (1972) The Origin and Structure of Easterly Waves in the Lower Troposphere of North Africa, Journal of the Atmospheric Sciences
The issue of convection is still actively studied, with interesting results:
Mekonnen, et.al (2006) Analysis of Convection and Its Association with African Easterly Waves, Journal of Climate
So, what initiates convection? An unstable atmospheric profile leads to convection, but what controls the timing? Small and unpredictable perturbations. While most perturbations will lead to no effect, some will initiate processes that had already built up a thermodynamic potential. That is not really about the propagation of energy through the atmosphere. Consider a large avalanche triggered by a small pebble – or by a slight increase in temperature. The initial energy is irrelevant relative to the final effect. It is the timing that matters here in terms of predictability at large scales.
Getting back to our concrete example, a train of easterly waves forms over Africa each year from with a periodic component of 3-5 days. Butterfly-triggered convection plays a role in the timing of the irregular component. (Type convection + chaos into any science publication search engine and you’ll get thousands of hits.)
Each member of this train of generated easterly waves may or may not amplify into anything, depending on the net state of the Atlantic Warm Pool, such as sea surface temps and depth of the warm surface layer, and the atmospheric wind shear above it. Each easterly wave represents, after Kerry Emanuel: “A subcritical bifurcation of the radiative-convective equilibrium state.” Any butterfly energy involved in initiating the wave dissipated long ago.
The perturbation doesn’t have to amplify into a hurricane. There are many kinetic pathways that will resolve the thermodynamic potential that backs up a major hurricane without actually forming a hurricane. In other words, only a small fraction of the net energy released via the evaporation/condensation water cycle over the Atlantic organizes into hurricanes. Isaac Held probably knows, journalists.
However, warm the atmosphere, warm the oceans, and you increase sea surface temps as well as the moisture content of the atmosphere, thereby forcing two of the thermodynamic parameters behind hurricane formation. There is more latent energy in the system, in other words, unless some other parameters act to counteract that (external wind shear, say). Will the fraction of energy that organizes itself into hurricanes remain constant? If so, you would expect the frequency and/or intensity of hurricanes to increase, regardless of their specific and irregular timing.
Well, the oceans and sea surface temps have definitely warmed up. After Rayner et. al (2006):
Accuweather and a few others. are still trying to claim, with no backing evidence, that this due to a “warm water cycle” in the Atlantic – and are being quoted on that by Reuters and other wire services.
The point here is that broad statements about the climate being chaotic or not are always misleading. Every real physical system has regular and irregular components; analyzing that allows one to get a handle on the limits of predictability for the system over different timescales.
> very large number of possible future atmospheric states
But not going off into infinity in all directions, gathering around
http://en.wikipedia.org/wiki/Image:Lorenz_attractor_yb.svg
as mentioned in the original post
Excuse me for my ignorance, but is the following anywhere near target?
Butterfly flap can
1. have little or no effect beyond the perturbation of the surrounding air
2. have considerable effect if that flap contributes to and is essential for a cascading effect– in which case other conditions are as essential. If any one of the necessary conditions were missing, then possibly no large scale event might occur. How we might “rank” conditions as to importance and to effect might be instructive.
In either case, to ascribe to the flap the primary creation of an event larger than itself is certainly a mistake. Note I said, “primary creation.”
[Response: None of this is right. The influence of the butterfly on the surrounding air propagates to larger scales and eventually affects the entire atmosphere. The thought experiment is starting with two identical atmospheres, which differ only by the flap of the butterfly wing. The claim is that even the large scale winds (e.g. position of a tornado or hurricane, or even onset of an El Nino) will diverge between the two realizations, given sufficient time. Regarding point (2), the general understanding of chaos is that you don’t need special conditions in the atmosphere for a “cascade” to occur leading to sensitive dependence on initial conditions. The sensitivity is generic to any sufficiently complicated nonlinear system, of which the atmosphere is almost certainly an example (though not yet provably so, in the rigorous mathematical sense). In fact Ruelle showed that (in a strict sense) “almost every” system with 5 or more degrees of freedom has a strange attractor in its dynamics. Thus, you should turn (2) around: the situation is that VERY SPECIAL conditions would have to occur to avoid a cascade leading to sensitive dependence. Now mind you, for any given specified nonlinear system, it has proved difficult or impossible for mathematicians to rigorously prove the existence of a strange attractor. This has been done for several special classes of systems, but partial differential equations pose a severe challenge. Last time I checked, it wasn’t even rigorously proved that the Lorentz/Saltzman equations had a strange attractor, though from the numerical behavior the truth of the assertion is not seriously in doubt. We are all physicists here, and need to do things even in areas where the mathematical challenge of rigorous proof has not yet been satisfied. No surprise there. Airplanes are designed on the basis of Navier Stokes all the time, even though it hasn’t yet been proved that solutions exist and are unique. –raypierre]
More than just the occasionnal butterfly, one has to look at drifting snow or sand streams, in the hundreds per Kilometer, all undulating differently stretching for Kilometers, just to realize that its a pipe dream to come up with a model capable of replicating each wind stream correctly for each future moment. The argument about heat is a better one, I think we can measure the temperature of the entire atmosphere, at least I do that myself at 2 locations. It is a climate metric, far more easier to measure, trend and predict, yet, I see very little of it out there. Must thank Lorenz nevertheless for showing our limitations. Now can we manage to do what we can?
I really liked Ed Lorenz and have tremendous respect for him. He was a friend of my advisor and came around a few times when I was a grad student.
But one point; probably futile, but before there was the “Butterfly Effect” is was called the “Seagull Effect”, but it did not become as popular. My advisor explained the origin to me was an address that G. D. Robinson gave, I think some sort of presidential address to a 1965 WMO meeting, if memory serves about the limits of weather prediction. Robinson referred to the (then well-known) transfer of information from small length scales to large length scales and the overturning time of the atmosphere (about three days) asking whether in order to predict weather for more than a week we would need to observe every flap of a seagull’s wing on the other side of the globe.
Is this the same as the “butterfly effect”? I think so. because at the time, it was well understood that on short length scales, atmospheric turbulence is like 3-D homogeneous turbulence then it’s really clear that neither the seagull nor the butterfly are going to be monitored for the five day forecast. So the small scale mixing gets rid of the effect of any single small event.
What then was the preoccupation with this question in 1965? The real issue was not that a single event on a small scale could result in hurricanes on the other side of the world. The real issue was that there was coupling from those length scales to larger length scales, which is in some sense the gist of the school of thought of Kolmogorov/Obukhov, Batchelor, Kraichnan, and Leith (etc). In some sense it’s the Fourier coefficient of the flow field at the high wavenumbers which matters, so it is a sort of collective organization of information at that spatial scale that matters. And in some sense, what you do about that is figure out how to solve the problem only on the large spatial scales without your solution implicitly violating what has to occur at the spatial scales which you wish were beneath your notice. You do not have to have either the butterfly or seagull traffic reports on your desk. And this was to some extent Robinson’s point. They knew then they didn’t have to birdwatch to forecast.
[Response: The history linked in the original post gives the history of the metamorphosis of the seagull (1963) to the butterfly (1972). – gavin]
John Nielsen-Gammon: “Lorenz’s oral presentations were also marvels of astonishing clarity.”
Yes they were. You just had to sit close and listen hard. People like to talk about Lorenz as a guy who had this great phenomenon drop in his lap. He was lethally intelligent, and didn’t miss tricks. He had many important ideas and contributions, and he usually knew exactly what he was doing.
Raypierre’s response to #33 suggests an interesting solution to the problem of global warming.
We just need to find the butterfly in the jar in that room and kill it.
[Response: I think you’d find that no amount of butterfly-killing (not that I’d advocate that anyway) would offset the effects of a change in the global radiation budget. There are somethings you just can’t control by controlling the noise. Now, if you were talking about weather control, you’d be in a different ball game. There is a considerable literature on control of chaotic systems, exploiting the fact that there is a window of time where you can actually use the sensitive dependence to initial conditions to control the future state with little expenditure of energy. This was worked out explicitly for the chaotic pendulum, but a few years ago, as a joke, I suggested to the clever folks at the Beckman Institute at U. of Illinois (Urbana-Champaign) that you could perhaps control the Pacific storm track the same way. In fact, they took me quite seriously, and I wound up putting together a talk on the subject, though the idea never got picked up and explored in a rigorous way. The question is: how much could you control storms in the Pacific storm track through a controlled variation of the surface energy budget by,say, a tenth of a W/m**2 applied over 10,000 km**2 near the origin of the storm track? It’s quite routine these days to do similar things with control of turbulence on the laboratory scale. –raypierre]
Re #35, Ray says “what will clouds really do?”. That’s where I am wondering what the models really do. The clouds are resulting from the weather, currently mainly from the negative NAO here in Virginia. There are low and middle clouds which are probably climate neutral but also some blow-off high clouds from yesterday’s thunderstorms and the jet stream (generally climate cooling). Like I said above, these climate effects are not “averaged out” or offset by climate effects elsewhere. However, I can envision that the NAO can be modeled based on other statistics in the climate models (mainly SST). That should give an accurate depiction despite its highly nonlinear and chaotic origins.
But there are other smaller scale effects on clouds that require similar parameterization to be accurately modeled. These are things like warm weather convection and cyclogenesis in various temperatures. The climate effects of the resultant clouds are concentrated convection (cooling), warming from low clouds, cooling from high clouds, and others (see http://www.ccsm.ucar.edu/publications/PhD%20and%20Masters%20Theses.htm) My question is can the chaotic effects be parameterized or modeled directly, particularly at the mesoscale?
I only knew of Lorenz’s work at second hand, but he was clearly a scientist of great significance, and from what’s been said here, a fine human being. On both counts, a sad loss.
I think I remember reading in New Scientist a few years ago, that the rate at which weather models diverged from the real weather was not in fact exponential, suggesting that flaws in the models rather than sensitivity to initial conditions was, at that time, the main cause of inaccuracy. This was, if I recall rightly, presented as grounds for optimism about future progress in weather forecasting. Anyone else remember this?
[Response: I didn’t see the New Scientist article, but Lorenz himself started off an inquiry of this sort in the 1980’s during a sabbatical at the European Center for Medium Range Weather Forecasting. By a clever study of forecast performance as a function of successive time lags, it was concluded that, at the time, forecast error 5 days out was still dominated by systematic error — model errors leading to climate drift — rather than the intrinsic predictability decay. That was good news, because it meant that the medium range predictability limit had not yet been reached, and science could still improve medium range forecasts. I haven’t followed this area very closely in the subsequent years, so I don’t know where the matter stands at the moment. Perhaps one of our readers can provide an update. The problem of climate drift was one that bedeviled ocean-atmospere models for a long time, but the better ones seem to have gotten it under control, at least on the time scale of a few centuries. –raypierre]
Having read raypierre’s last reply that even an educated climate science layman can appreciate, I have to wonder if Roger A. Pielke Sr. has crossed a line here. I can fully appreciate the contributions of Edward Lorenz in the field of the numerical analysis of dynamic systems, and his discovery of the vividly named and startlingly non-intuitive “butterfly effect” is an inspiration to anyone interested in mathematics and the sciences. But during the course of Pielke’s arguments on scale of phenomena and their effects on the atmosphere, I begin to wonder if we should call for the expertise of a lepidopterist to inform us of how many butterflies may fit on the head of a bowling pin.
Unfortunately having to step back from the realm of science into that of the political, it would seem that Roger A. Pielke Sr. has selected this line of debate precisely because Lorenz’s discovery is counter-intuitive and therefore its refutation is appealing to the pseudo-common sense of the global warming deniers. Despite the credibility granted to Pielke by the editors of Nature, his belief that heat at the surface of the Earth may be radiated away without any expanding effect on the surrounding atmosphere makes this reader wonder if he is any longer worthy of the space afforded to him in his tedious arguments.
My apologies for having to bring up this point in a blog dedicated as tribute to the life of Edward Lorenz. Of course the ultimate decision rests with the owners of RealClimate, and in answering Pielke’s latest salvos they have once again provided an excellent service to their readers.
[Response: I wouldn’t want to guess at Roger Sr’s motives, but I’d avoid explaining by conspiracy what could be more easily be explained by confusion and bad judgment. Also, I’ll emphasize that with regard to chaos and Lorenz, Roger and I probably agree on more than we disagree on. I do think it is fair to keep in mind the scientifically indefensible tenor of some of Roger’s arguments here when judging how much credence to give the stuff Roger publishes on his blog — for example the recent guest post by Spencer, about which I’ll me commenting in the next few weeks. By the way, regarding your comment on Nature, are you perhaps confusing Roger Sr with Roger Jr? Or which article did you have in mind? –raypierre]
Re: Reponse to my 45: “I didn’t see the New Scientist article, but Lorenz himself started off an inquiry of this sort in the 1980’s during a sabbatical at the European Center for Medium Range Weather Forecasting. – raypierre
I’m probably remembering a New Scientist report of that inquiry. You know you’re well into middle age when two decades seems like “a few years”!
You are correct in that you and I probably agree on most issues in chaos and nonlinear dynamics. All NWP and climate models show the sensitivity of large scale circulation features to initial conditions when perturbations are inserted in their initial state or in their parameterizations (these are all much larger effects than the energy that a butterfly places in the system). We also agree that the added heat from a butterflies flapping wings results in a slightly different system than if this flapping did not occur. However, the issue is whether the heat (the “information”) from this effect can translate (teleconnect) to larger scale so as to result in alterations in large scale features.
Even Issac Held seemed to indicate that there is a lower limit to when this upscale effect can occur (i.e. this ability disappears when the flow becomes laminar); he said in this thread
“the scale of the perturbation has to be larger than what is often referred to as the Kolmogorov microscale, the scale below which the flow is effectively laminar, to avoid being damped out immediately. This scale is typically a few millimeters in the atmosphere….”
I agree with this, but maintain that the smallest turbulent scales also are damped out due to the physics of non-motion transfers (i.e. radiative transfers) of energy. I have been in communication with Professor Ekyholt on this question, and he and I agree that you are misinterpreting the butterfly effect for very small scale perturbations. We will be preparing a paper on this to demonstrate that there is lower limit to which the “butterfly effect” applies.
On a separate note, I see commenters on this thread are somehow skewing this discussion to be on climate change. It is not. This issue of the scale at which the “butterfly effect” occurs is a pure discussion of the science such as we all used to have as graduate students and need more of!
Also, you questioned as to why Roy Spencer posted a guest weblog. The answer is that he has introduced a novel and important new perspective into how variations in atmospheric/ocean circulations can result in alterations in the global average radiative balance. Disagreements with his results and conclusions should be on his science. I invite others (including any interested Real Climate climate scientist) to post unedited guest weblogs on Climate Science
Ray – In searching for what Professor Lorenz has said on this issue, please see “Chaos Avant-Garde: Memories of the Early Days of Chaos Theory”
http://books.google.com/books?hl=en&lr=&id=0E667XpBq1UC&oi=fnd&pg=PA91&dq=butterfly+effect&ots=VUaNFd67Be&sig=gQh5rcXesTIokMPZeT1qYmHh36g#PPA94,M1
In this essay he writes,
“Returning now to the question as originally posed, we notice some additional points not yet considered. First of all, the influence of a single butterfly is not only a fine detal – it is confined to a small volume. Some of the numerical methods which seem to be well adapted for examining the intensification of errors are not suitable for studying the dispersion of errors from restricted to unrestricted regions. One hypothesis, unconfirmed, is that the influence of a butterfly’s wings will spread in turbulent air, but not in calm air”
This certainly would rule out the butterfly in the jar! More importantly, he recognized that there remain questions about the “butterfly effect”, one of which is when small pertubations result in altering larger scale atmospheric flow, and when they do not.
[Response: I’ve said all I’m going to say about this issue. I think the implications of conservation of energy, and of the effect of the heating of surrounding air by dissipation of mechanical energy, are pretty clear. You are putting your own construction on Lorenz’s words. –raypierre]
My apologies for skipping over many comments for lack of time – I may come back later to finish, but I wanted to jump in on a few points.
Re 19 – that’s a very interesting point. It occurs to that it may be a matter of probability – a random pertubation would have almost no chance of having no component in the expanding dimension. Then I can imagine a class of perturbations that initially shrink (if dominated by the contracting component) before growing again (as the contracting component becomes smaller than the other component). Presumably this can be generalized to strange attractors in phase spaces of n-dimensions.
Re 48 – it occurs to me that this may be a matter of probability – if the heat generated by a perturbation’s thermal damping is contained by just one molecule, and can be emitted by a single photon (before any molecular collisions), and that single photon manages to escape to space, then some of the perturbation has been ‘lost’ (but what if it reflects off the moon and comes back, or knocks into a dust grain – after some time, the dust grain is in a different position, perhaps it causes some other dust grain to fall back to earth and a butterfly notices it… granted, I had to go outside the system, there) but there is still the recoil of the photon-emitting particle. Anyway, the molecule may be oriented differently… And the effects on the gravitational field, and the electromagnetic field of the molecule … and then, what if a person sees the butterfly (okay, I’ve gone out of the system again – but on that note, presumably the butterfly has been affected by it’s own flap, so the effects of it’s future flaps have been altered). It seems to me their is always some lingering microscopic alteration that has some potential to grow at a later time. Quantum uncertainty may make the effects of the smallest perturbations somewhat superfluous, I think.
—
Could a climate phase space be constructed with modes of internal variability being used as dimensions? I’d like to see that.
I enjoy thinking about attractors in phase space. It occurs to me that for n degrees of freedom (all the properties of every particle), one might be able to compress the description of the state of a system down to m degrees of freedom (the conditions of air parcels of meter size) by settling for an approximation – in which case, the trajectories become somewhat probabilistic. One might map the phase space into a different phase space where features of the attractor are used as dimensions. Climate change could involve both translation of the attractor and distorting it, so I wonder if, for example, not just the variability along a mode of internal variability, but the mode’s shape, may change… Of course this is common sense now, but it’s fun to think about in that way. One helpful point is that at sufficiently small scale, all trajectories are locally nearly parallel. I like to use the distinction between weather and climate (sensitivity to initial conditions vs determined by boundary conditions) to use the terms in a generalized way – one might think of the weather and climate of mantle convection, of ecosystems, of evolution, of economies, of galaxies – climate might even apply just in space, where the climate would be a generalized texture… (On a related note, I’ve wondered how it would look if one modelled the atmosphere as an ecosystem, with different populations of ‘organisms’ (some of which may be endosymbionts of others…) And they can vary on different scales – climate for a short-lived bacterium (a snowstorm, individual weather events are snowflakes) may be weather for a human; etc. In that sense, conditions might be approximated as boundary conditions in the short term (sea surface temperatures, for weather) but in the longer term must be included as variables in a larger (in terms of dimensions, any way) system. Speaking of which, if the limit of predictability of the atmosphere is 2 weeks, I’m curious what it is for the ocean (realizing that may depend on the particular aspect or part), river meanderings, mantle convection, the outer core (and thus, magnetic field)?
So thanks to Ed Lorenz for writing about chaotic behavior! PS I thought the butterfly came from the shape of the attractor.
I’d love to hear more about “resonant triad instability”.